遗传算法 ( GA ) 指的是启发性算法 ( EA ),主要应用于其分析解法十分困难或甚至不可能的问题,它在大多数具有现实意义的情形中给出问题的可接受解决方案,但决策的正确性没有经过数学证明。
此类(NP 类)问题的一个经典例子是“旅行商问题”(最著名的组合优化问题之一)。该问题的主要挑战在于找出最有利的路线,通过给定的城市至少一次后回到出发城市。但不会影响把它们用于囿于形式化的任务。
EA 被广泛用于解决具有高度计算复杂性的问题,而不是一一尝试所有选项,这将耗费大量的时间。它们被应用于人工智能领域(如模式识别)、杀毒软件、工程、电脑游戏和其他领域。
值得一提的是,MetaQuotes Software Corp. 在其 MetaTrader 4/5 的软件产品中使用了 GA。我们都知道策略测试程序,也知道使用内置的策略优化程序可以节省大量的时间和精力,正如在其中使用直接枚举优化 GA 的应用是可能的。此外,MetaTrader 5 测试程序允许我们使用用户优化标准。可能读者会有兴趣阅读一些有关 GA 的文章,并对相比 直接枚举 EA 可提供哪些优势感兴趣。
就在一年前,我亟需一个优化算法用于训练神经网络。在快速地了解各种算法后,我选择了 GA。然而在搜索现成实施后,我发现对公众开放的算法要么就具有功能限制(如可优化的参数的数量),要么就是“可自己发挥的空间”太小。
我需要的是具有普适性的灵活工具,不仅可用于训练所有类型的神经网络,亦可用于任何优化问题的一般性求解。在对陌生的“遗传资料”长期研究后,我仍然无法理解它们是如何工作的。造成这种情况的原因可能是复杂的代码风格,或是我缺乏编程经验,或两者皆有之。
困难主要来自于将基因编码为二进制代码以及以这种形式使用它们。无论哪种方式,都需要从头开始编写遗传算法,将重点放在可量测性和未来易于修改上。
我不想进行二进制转换,并决定直接使用基因,即,以实数的形式通过基因组来表示染色体。这就是我使用实数表示染色体的遗传算法的代码问世的过程。后来我才知道,这并不是什么新的发现,类似的遗传算法(称为实数编码 GA)自从它们首次被发布出来已超过 15 年。
我把我探索 GA 功能的实施和原理的构想留待读者评定,因为这是基于它在实际问题中使用的个人经验。
GA 蕴含的原理借鉴于大自然本身。它们是遗传和变异的原理。遗传是生物将它们的生物特性和进化特征传递给后代的能力。由于这种能力,所有生物才能将它们的物种特性留给它们的后代。
生物的基因变异保证了种群的遗传多样性,并且变异是随机的,因为大自然无法提前得知哪些特征在未来是最合适的(气候变迁、食物的增加/减少、竞争物种的出现等)。变异使生物出现新的性状,从而能够在新的、变化的栖息条件下生存和留下后代。
在生物学中,由于突变引起的变异称为突变,而通过交配实现基因的进一步交叉组合所引起的变异称为组合。GA 中有这两种变异类型的实施。此外,还有突变的实施,模仿于突变的自然机制(DNA 的核苷酸序列发生变化)- 自然(自发)和人工(诱变)。
按照算法的准则,信息传递的最简单的单位是基因 - 遗传的结构和功能单位,控制特定的性状和属性的发展。我们将函数的一个变量称之为基因。基因通过实数来表示。基因组 - 所研究函数的变量是染色体的表征特征。
我们同意以列的形式表示染色体。则函数 f (x) = x ^ 2 的染色体将如下图所示:
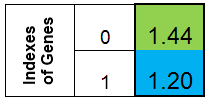
图 1. 函数 f (x) = x ^ 2 的染色体
其中,第 0 个索引 - 函数 f (x) 的值,称为个体的适应度(我们将该函数称之为适应度函数 - FF ,将函数的值称之为 - VFF )。染色体可方便地存储于一维数组中。即,double Chromosome [] 数组。
所有进化同代的样本组成一个种群。此外,种群将随意地分为两个相等的群体 - 上代群体和后代群体。执行上代物种(从整个种群中选出)的交叉以及 GA 的其他算子后,我们将得到一个新的后代群体,其规模为种群规模的一半,并将取代种群中的后代群体。
在搜索函数 f (x) = x ^ 2 最小值的期间全体个体种群可能如下图所示:
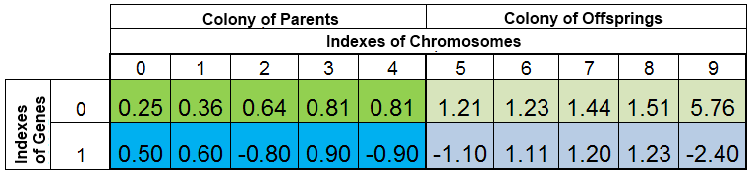
图 2. 全体个体种群
种群通过 VFF 存储。在这里,染色体的第 0 个索引被具有最小 VFF 的样本占据。新的后代完全取代后代群体中的个体,而上代群体保持不变。然而,上代群体不是始终保持完整的,因为重复的样本将被销毁,然后新的后代将填充上代群体中的空缺,剩余的则填充至后代群体中。
换言之,种群规模保持恒定的情况是很罕见的,因年代而变,这几乎和大自然是一样的。例如,在繁殖前后种群可能如下图所示:
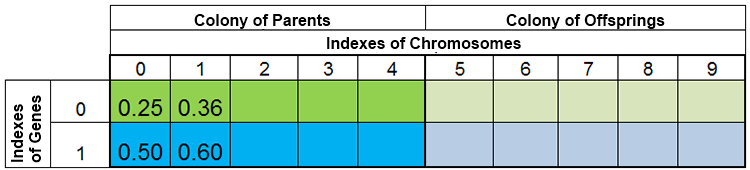
图 3. 繁殖前种群
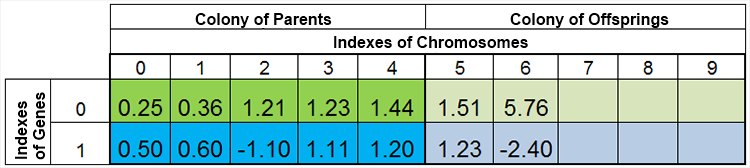
图 4. 繁殖后种群
描述的通过后代“半”实现种群的机制以及销毁重复的染色体和禁止个体与自身杂交都只有一个目的 - 那就是避免“瓶颈效应”(生物学中的一个术语,意思是多种不同因素造成的临界减少所引起的种群基因库的缩减可导致物种的完全灭绝。GA 面临着不再出现唯一染色体、在某个局部最优解“卡住”的情形)。
针对指定数量的一代,从步骤 5 开始重复执行此过程,直到没有优于参考染色体的染色体出现。
3.1. 全局变量全局变量
从全局层面声明以下变量:
//----------------------全局变量----------------------------- double Chromosome[]; //函数的一系列优化的参数 - 染色体的基因 //(例如: 神经网络的权重, 等等) int ChromosomeCount =0; //种群中的最大可能染色体数量 int TotalOfChromosomesInHistory=0;//历史中的染色体数量 int ChrCountInHistory =0; //染色体库的染色体数 int GeneCount =0; //染色体的基因数 double RangeMinimum =0.0;//最小搜索范围 double RangeMaximum =0.0;//最大搜索范围 double Precision =0.0;//搜索步长 int OptimizeMethod =0; //1-最小值, 其他任意值 - 最大值 int FFNormalizeDigits =0; //适应值的小数点位数 int GeneNormalizeDigits =0; //基因值的小数点位数 double Population [][1000]; //种群 double Colony [][500]; //后代群体 int PopulChromosCount =0; //种群中当前染色体数目 int Epoch =0; //未进化代数 int AmountStartsFF=0; //适应函数启动次数 //————————————————————————————————————————————————————————————————————————
3.2. UGA.GA 的主函数
实际上,从程序的主体调用以执行相关步骤的 GA 的主函数已在上文中列示,因此我们不会在此讨论过多的细节。
待算法完成后,将以下信息记录在日志中:
“唯一染色体的数目”和“FF 启动的总次数”- 规模相同,计算方法不同。用于控制。
//———————————————————————————————————————————————————————————————————————— //UGA 基本函数 void UGA ( double ReplicationPortion, // 复制的比例. double NMutationPortion, // 自然突变比例. double ArtificialMutation, // 人工突变比例. double GenoMergingPortion, // 借用基因比例. double CrossingOverPortion, // 交叉部分. //--- double ReplicationOffset, // 区间边界转换系数 double NMutationProbability // 每个基因可能发生突变的百分率 ) { //只做一次生成器重置 MathSrand((int)TimeLocal()); //-----------------------变量------------------------------------- int chromos=0, gene =0;//染色体和基因的索引 int resetCounterFF =0;//"没有进展的世代"的重置计数器 int currentEpoch =1;//当前世代的编号 int SumOfCurrentEpoch=0;//"没有进展世代"的总数 int MinOfCurrentEpoch=Epoch;//"没有进展世代"的最小值 int MaxOfCurrentEpoch=0;//"没有进展世代"的最大值 int epochGlob =0;//世代总数 // Colony [特性数(基因数)][种群中的个体数] ArrayResize(Population,GeneCount+1); ArrayInitialize(Population,0.0); // 下代种群 [特性数(基因数)][种群中的个体数] ArrayResize(Colony,GeneCount+1); ArrayInitialize(Colony,0.0); // 染色体库 // [特性数 (基因数)][库中的染色体数] double historyHromosomes[][100000]; ArrayResize(historyHromosomes,GeneCount+1); ArrayInitialize(historyHromosomes,0.0); //---------------------------------------------------------------------- //--------------验证输入参数的正确性---------------- //...染色体总数必须大于等于 2 小于等于 500 if(ChromosomeCount<=1) ChromosomeCount=2; if(ChromosomeCount>500) ChromosomeCount=500; //---------------------------------------------------------------------- //====================================================================== // 1) 创建原始种群 —————1) ProtopopulationBuilding(); //====================================================================== // 2) 确定每个个体的适应性 —————2) //对于第一个群体 for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=0;chromos<ChromosomeCount;chromos++) Population[0][chromos]=Colony[0][chromos]; //对于第二个群体 for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos-ChromosomeCount]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) Population[0][chromos]=Colony[0][chromos-ChromosomeCount]; //====================================================================== // 3) 准备种群进行繁殖 ————3) RemovalDuplicates(); //====================================================================== // 4) 展开染色体参考 —————4) for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; //====================================================================== ServiceFunction(); //基因算法的主循环 从第 5 步到第 6 步 while(currentEpoch<=Epoch) { //==================================================================== // 5) UGA 算子 —————5) CycleOfOperators ( historyHromosomes, //--- ReplicationPortion, //复制的比例. NMutationPortion, //自然突变的比例. ArtificialMutation, //人工诱变的比例. GenoMergingPortion, //外来的基因比例. CrossingOverPortion,//交叉比例. //--- ReplicationOffset, //区间边界转换系数 NMutationProbability//每个基因突变可能性百分比 ); //==================================================================== // 6) 比较最佳后代的基因和参照染色体的基因. // 如果最佳后代的染色体比参照染色体好, // 替换掉参照染色体. —————6) //如果优化模式为 - 最小化 if(OptimizeMethod==1) { //如果种群的最佳染色体比参照染色体好 if(Population[0][0]<Chromosome[0]) { //替换掉参照染色体 for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //重置 "无进展世代" 计数器 if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //如果优化模式为 - 最小化 else { //如果种群的最佳染色体比参照染色体好 if(Population[0][0]>Chromosome[0]) { //替换掉参照染色体 for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //重置 "无进展世代"计数器 if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //==================================================================== //另一个世代来临.... epochGlob++; } Print("到来世代=",epochGlob," 重置次数=",resetCounterFF); Print("MinOfCurrentEpoch",MinOfCurrentEpoch, " AverageOfCurrentEpoch",NormalizeDouble((double)SumOfCurrentEpoch/(double)resetCounterFF,2), " MaxOfCurrentEpoch",MaxOfCurrentEpoch); Print(ChrCountInHistory," - 唯一染色体"); Print(AmountStartsFF," - 适应性函数运行总数"); Print(TotalOfChromosomesInHistory," - 历史中的染色体总数"); Print(NormalizeDouble(100.0-((double)ChrCountInHistory*100.0/(double)TotalOfChromosomesInHistory),2),"% 重复"); Print(Chromosome[0]," - 最佳结果"); } //————————————————————————————————————————————————————————————————————————
3.3. 创建一个原型种群。创建一个原型种群。
由于在大多数优化问题中,我们无法提前得知函数自变量分布于数值轴的位置,因此最佳的优化选项是在给定范围内随机生成。
//———————————————————————————————————————————————————————————————————————— //创建原始种群 void ProtopopulationBuilding() { PopulChromosCount=ChromosomeCount*2; //使用染色体随机填充种群 //...基因范围在 RangeMinimum...RangeMaximum 之间 for(int chromos=0;chromos<PopulChromosCount;chromos++) { //从索引 1 开始 (索引 0 为 VFF 保留) for(int gene=1;gene<=GeneCount;gene++) Population[gene][chromos]= NormalizeDouble(SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); TotalOfChromosomesInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.4. GetFitness.获取适应度
按顺序针对每个染色体执行优化函数。
//------------------------------------------------ ------------------------ // 获取每个个体的适应度. void GetFitness ( double &historyHromosomes[][100000] ) { for(int chromos=0;chromos<ChromosomeCount;chromos++) CheckHistoryChromosomes(chromos,historyHromosomes); } //————————————————————————————————————————————————————————————————————————
3.5. CheckHistoryChromosomes.通过染色体库验证染色体
通过染色体库验证每个个体的染色体 - 无论 FF 是否已为其计算,如果是,则从库中提取现成的 VFF,如果不是,则为其调用 FF。因此,我们可以将 FF 重复的资源密集型计算排除在外。
//———————————————————————————————————————————————————————————————————————— //通过染色体库验证染色体. void CheckHistoryChromosomes ( int chromos, double &historyHromosomes[][100000] ) { //-----------------------变量------------------------------------- int Ch1=0; //库中的染色体索引 int Ge =0; //基因索引 int cnt=0; //唯一基因计数器. 如果至少有一个基因不同 //- 染色体就被认为是唯一的 //---------------------------------------------------------------------- //如果染色体库中至少有一个染色体 if(ChrCountInHistory>0) { //枚举库中染色体以寻找相同的那个 for(Ch1=0;Ch1<ChrCountInHistory && cnt<GeneCount;Ch1++) { cnt=0; //当基因索引小于基因总数且有相同基因时比较基因 for(Ge=1;Ge<=GeneCount;Ge++) { if(Colony[Ge][chromos]!=historyHromosomes[Ge][Ch1]) break; cnt++; } } //如果没有足够的相同基因, 我们可以使用库中准备好的方法 if(cnt==GeneCount) Colony[0][chromos]=historyHromosomes[0][Ch1-1]; //如果没有这样的染色体, 我们则计算它的适应性函数... else { FitnessFunction(chromos); //.. 如果基因库中有空间, 就保存它 if(ChrCountInHistory<100000) { for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } } //如果基因库为空, 计算它的适应性函数并且在库中保存它 else { FitnessFunction(chromos); for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.6. CycleOfOperators.UGA 中算子的循环
整整一代人工生命的命运至此已盖棺定论 - 新的一代出生,然后死亡。这通过以下方式实现:选择双亲进行交配,或选择一个亲本实施突变。为 GA 的每个算子确定适当的参数。如此一来,我们获得一个后代。这一过程不断重复,直到完全填充后代群体。然后,后代群体进入生境,这样每个个体能够尽可能地展示自己,然后我们计算 VFF。
在经过各种“生存”考验后,后代群体融入种群中。人工进化的下一步将是毁灭克隆体,以防止“血统”在子孙后代中耗尽,并根据适应度对进化的种群排序。
//———————————————————————————————————————————————————————————————————————— //UGA 算子循环 void CycleOfOperators ( double &historyHromosomes[][100000], //--- double ReplicationPortion, //复制的比例. double NMutationPortion, //自然突变的比例. double ArtificialMutation, //人工突变的比例. double GenoMergingPortion, //借用基因比例. double CrossingOverPortion,//交叉比例. //--- double ReplicationOffset, //区间边界转换系数 double NMutationProbability//每个基因突变可能性百分率 ) { //-----------------------变量------------------------------------- double child[]; ArrayResize (child,GeneCount+1); ArrayInitialize(child,0.0); int gene=0,chromos=0, border=0; int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,6); ArrayInitialize(fit,0.0); //新种群植入点计数器. int T=0; //---------------------------------------------------------------------- //设置 UGA 算子的比例 double portion[6]; portion[0]=ReplicationPortion; //复制比例. portion[1]=NMutationPortion; //自然突变比例. portion[2]=ArtificialMutation; //人工突变比例. portion[3]=GenoMergingPortion; //借用基因比例. portion[4]=CrossingOverPortion;//交叉比例. portion[5]=0.0; //------------------------ UGA 算子循环 --------- //把后代群体填入种群 while(T<ChromosomeCount) { //============================ for(i=0;i<6;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(portion[i]-portion[5]); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[4][1]); for(u=0;u<5;u++) { if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; } //============================ switch(u) { //--------------------- case 0: //------------------------复制-------------------------------- //如果新群体有空间, 创建一个新个体 if(T<ChromosomeCount) { Replication(child,ReplicationOffset); //把新个体加入新群体中 for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //占用一个位置, 增加计数器 T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 1: //---------------------自然突变------------------------- //如果新群体有空间, 创建一个新个体 if(T<ChromosomeCount) { NaturalMutation(child,NMutationProbability); //把新个体加入新群体中 for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //占用一个位置, 增加计数器 T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 2: //----------------------人工诱变----------------------- //如果新群体有空间, 创建一个新个体 if(T<ChromosomeCount) { ArtificialMutation(child,ReplicationOffset); //把新个体加入新群体中 for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //占用一个位置,增加计数器 T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 3: //-------------使用借用基因创建个体----------- //如果新群体有空间, 创建一个新个体 if(T<ChromosomeCount) { GenoMerging(child); //把新个体加入新群体中 for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //占用一个位置,增加计数器 T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- default: //---------------------------交叉--------------------------- //如果新群体有空间, 创建一个新个体 if(T<ChromosomeCount) { CrossingOver(child); //把新个体加入新群体中 for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //占用一个位置, 增加计数器 T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- } }//UGA 算子循环结束-- //确定下代群体中每个个体的适应性 GetFitness(historyHromosomes); //把后代安排到主群中 if(PopulChromosCount>=ChromosomeCount) { border=ChromosomeCount; PopulChromosCount=ChromosomeCount*2; } else { border=PopulChromosCount; PopulChromosCount+=ChromosomeCount; } for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=0;gene<=GeneCount;gene++) Population[gene][chromos+border]=Colony[gene][chromos]; //为下一次繁殖准备种群 RemovalDuplicates(); }/函数结束 //————————————————————————————————————————————————————————————————————————
3.7. 复制复制
该算子与自然现象最为接近,在生物学中称之为 DNA 复制,虽然二者在本质上并相同。但我未找到任何在本质上要更为接近的对等物,所以我决定保留这个标题。
Replication 是最重要的遗传算子,它在传递亲本染色体的生物特性的同时产生新的基因。它也是确保算法收敛的主要算子。GA 仅使用这一个算子就能正常工作,但在这种情况下 FF 启动的次数将大为增加。
下面我们讨论 Replication 算子的原理。我们使用两个亲本染色体。新的后代基因是来自区间
[C1-((C2-C1)*ReplicationOffset),C2+((C2-C1)*ReplicationOffset)]
的随机数,其中 C1 和 C2 是亲本基因,ReplicationOffset 是区间边界 [C1, C2] 的位移系数。
例如,从父亲个体(蓝色)和母亲个体(粉色)可创建下代(绿色):
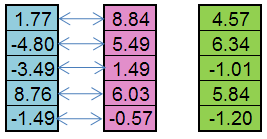
图 5. 算子 Replication 的工作原理
后代基因出现的几率可通过图形表示为:
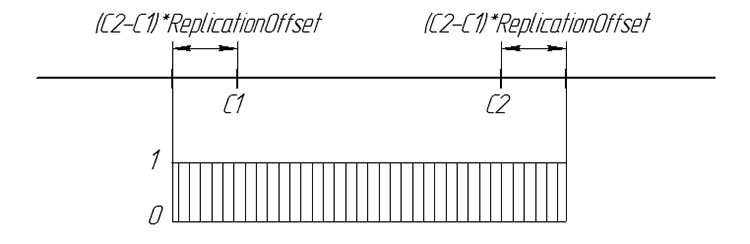
图 6. 数值轴上后代基因出现的几率
其他后代基因以相同的方式产生。
//------------------------------------------------ ------------------------ // 复制 void Replication ( double &child[], double ReplicationOffset ) { //-----------------------变量------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- SelectTwoParents(address_mama,address_papa); //-------------------基因枚举循环-------------------------------- for(int i=1;i<=GeneCount;i++) { //----找出父母的来源 -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //强制验证以确保搜索没有超过指定范围 if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....决定其中最大和最小的, //如果 С1>C2, 交换 if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //设置创建基因的边界 Minimum = C1-((C2-C1)*ReplicationOffset); Maximum = C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //强制验证以确保搜索没有超过指定的范围 if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- temp=RNDfromCI(Minimum,Maximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } //————————————————————————————————————————————————————————————————————————3.8. NaturalMutation.自然突变
突变在整个过程中于活细胞中不断发生,并为自然选择提供材料。突变自发地出现于正常生境条件下生物的整个生命过程中,频率为每 10 ^ 10 细胞世代发生一次。
作为有着强烈求知欲的研究人员的我们,不一定需要遵循自然次序,花费很长时间等待基因的下一次突变。NMutationProbability 参数可帮助我们实现这一点,它表现为一个百分比,确定染色体中每个基因的突变几率。
在 NaturalMutation 算子中,突变包含区间 [RangeMinimum, RangeMaximum] 中随机基因的生成。NMutationProbability = 100% 表示染色体中所有基因的突变几率为 100%,NMutationProbability = 0% 表示完全没有突变。最新的选项不适用于实际问题。
//------------------------------------------------ ------------------------ // 自然突变 void NaturalMutation ( double &child[], double NMutationProbability ) { //-----------------------变量------------------------------------- int address=0; double prob=0.0; //---------------------------------------------------------------------- if(NMutationProbability<0.0) prob=0.0; if(NMutationProbability>100.0) prob=100.0; //-----------------选择父母------------------------ SelectOneParent(address); //--------------------------------------- for(int i=1;i<=GeneCount;i++) if(RNDfromCI(0.0,100.0)<prob) child[i]=NormalizeDouble( SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits ); } //————————————————————————————————————————————————————————————————————————
3.9. ArtificialMutation.人工突变
该算子的主要任务是生成“新”血。我们使用两个亲本,并从数值轴上亲本基因未分配的空间选取后代的基因。保护 GA 以免过早收敛于某个局部最优解。相比其他算子,加速或减速收敛增加 FF 启动次数的可能性更大。
与 Replication 算子中一致,我们使用两个亲本染色体。但 ArtificialMutation 算子的任务不是将亲本的生物特性传递给后代,而是令后代与上一代有所不同。因此,作为一个完全对立的过程,我们使用 Replication 算子可能会采用的相同的区间边界位移系数,但基因在区间外生成。后代的新基因是来自于区间 [RangeMinimum, C1-(C2-C1) * ReplicationOffset] 和 [C2 + (C2-C1) * ReplicationOffset, RangeMaximum] 的随机数。
基因在后代 ReplicationOffset = 0.25 出现的几率可通过图形表示为:
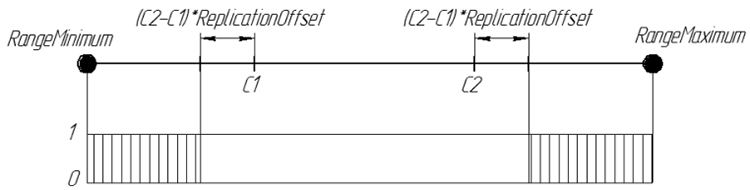
图 7. 基因在位于数值轴区间 [RangeMinimum; RangeMaximum] 上的后代 ReplicationOffset = 0.25 中出现的几率
//———————————————————————————————————————————————————————————————————————— //人工突变. void ArtificialMutation ( double &child[], double ReplicationOffset ) { //-----------------------变量------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0,p=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------选择父母------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //-------------------基因枚举循环------------------------------ for(int i=1;i<=GeneCount;i++) { //----决定父母的来源-------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //强制确认以确保搜索没有超过指定的范围 if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....决定其中最大和最小的, //如果С1>C2,我们改变它们的位置 if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //指定创建新基因的边界 Minimum=C1-((C2-C1)*ReplicationOffset); Maximum=C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //强制确认以确保搜索没有超过指定的范围 if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- p=MathRand(); if(p<16383.5) { temp=RNDfromCI(RangeMinimum,Minimum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } else { temp=RNDfromCI(Maximum,RangeMaximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } } //————————————————————————————————————————————————————————————————————————
3.10 GenoMerging.借用基因
该指定 GA 算子没有自然对等物。事实上,我们很难想象这一神奇的机制将如何作用于生物体上。然而,它具有将基因从多个亲本(亲本的数量等于基因的数量)传递至后代的显著特性。该算子不会生产新的基因,它是一个组合搜索机制。
其工作原理如下所示:针对第一个后代基因选择一个亲本,第一个基因从该亲本获得,然后,针对第二个基因选择第二个亲本,基因从该亲本获得,等等。如果基因的数量大于 1,应用该算子是明智的。否则,由于该算子将产生重复染色体,它将被禁用。
//———————————————————————————————————————————————————————————————————————— //借用基因. void GenoMerging ( double &child[] ) { //-----------------------变量------------------------------------- int address=0; //---------------------------------------------------------------------- for(int i=1;i<=GeneCount;i++) { //-----------------选择父母------------------------ SelectOneParent(address); //-------------------------------------------------------- child[i]=Population[i][address]; } } //————————————————————————————————————————————————————————————————————————
3.11. CrossingOver.交叉
交叉(在生物学中也称为杂交)是染色体相互交换片段的现象。与 GenoMerging 算子如出一辙,它是一个组合搜索机制。
选择两个亲本染色体。两个染色体分别取随机位置进行“切断”。后代染色体将由亲本染色体的片段组成。
展示该机制的最简单的方法莫过于使用图形:
图 8. 染色体片段的互换机制
如果基因的数量大于 1,应用该算子是明智的。否则,由于该算子将产生重复染色体,它将被禁用。
//———————————————————————————————————————————————————————————————————————— //交叉. void CrossingOver ( double &child[] ) { //-----------------------变量------------------------------------- int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------选择父母------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //决定突破点 int address_of_gene=(int)MathFloor((GeneCount-1)*(MathRand()/32767.5)); for(int i=1;i<=GeneCount;i++) { //----复制母亲基因-------- if(i<=address_of_gene+1) child[i]=Population[i][address_mama]; //----复制父亲基因-------- else child[i]=Population[i][address_papa]; } } //————————————————————————————————————————————————————————————————————————
3.12. SelectTwoParents.两个亲本的选择
为防止基因库枯竭,禁止个体与自身杂交。寻找不同亲本的尝试多达十次,如果寻找双亲失败,我们允许个体与自身杂交。从根本上来说,我们获得的是同一样本的副本。
一方面,降低了个体克隆的可能性,另一方面,阻碍了搜索的循环性,因为在某些情况下要通过合理数量的步骤实现这一点(选择不同的亲本)几乎是不可能的。
用于算子 Replication、ArtificialMutation 和 CrossingOver。
//———————————————————————————————————————————————————————————————————————— //选择两个亲本. void SelectTwoParents ( int &address_mama, int &address_papa ) { //-----------------------变量------------------------------------- int cnt=1; address_mama=0;//种群中母亲个体的位置 address_papa=0;//种群中父亲个体的位置 //---------------------------------------------------------------------- //----------------------------选择亲本-------------------------- //尝试10次选择不同的亲本. while(cnt<=10) { //对于母亲个体 address_mama=NaturalSelection(); //对于父亲个体 address_papa=NaturalSelection(); if(address_mama!=address_papa) break; } //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.13. SelectOneParent.一个亲本的选择
在这里,一切都很简单 - 从种群中选择一个亲本。
用于算子 NaturalMutation 和 GenoMerging。
//———————————————————————————————————————————————————————————————————————— //选择一个亲本 void SelectOneParent ( int &address//亲本个体在种群中的地址 ) { //-----------------------变量------------------------------------- address=0; //---------------------------------------------------------------------- //----------------------------选择一个亲本-------------------------- address=NaturalSelection(); //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.14. NaturalSelection.自然选择
自然选择 - 致使更好适应于这些环境条件、具有有用遗传性状的个体生存和优先繁殖的过程。
该算子与传统算子“轮盘”(轮盘选择 - 通过“转动”轮盘选择个体。种群中的每一个个体都在轮盘上具有相应的扇区。扇区的大小与个体对应的适应度值成比例)类似,但具有显著的不同。它将个体的位置考虑在内,即相对于最适应个体和最不适应个体的排位。此外,即使个体具有最差的基因,也有留下后代的机会。这很公平,不是么?虽然这无关公平,但事实上关乎大自然中所有个体都有机会留下后代的事实。
例如,在最大化问题中,取具有以下 VFF 的 10 个个体:256, 128, 64, 32, 16, 8, 4, 2, 0, -1 - 其中,较大的值对应更优的适应度。从该示例我们可以看出,相邻两个个体间的“距离”是前两个个体间的距离的三倍。然而,在饼形图上,每个个体留下后代的几率如下所示:
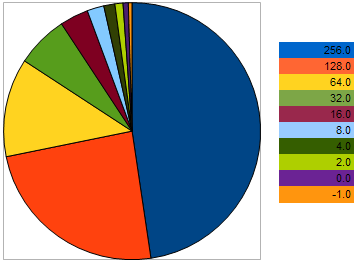
图 9. 选择亲本个体的几率图
通过上图我们可以看出,与适应性最差的个体越接近,个体留下后代的几率就越低。相反,个体与更好样本间的距离越小,其具有的繁殖几率越大。

图 10. 选择亲本个体的几率图
//———————————————————————————————————————————————————————————————————————— //自然选择. int NaturalSelection() { //-----------------------变量------------------------------------- int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,PopulChromosCount); ArrayInitialize(fit,0.0); double delta=(Population[0][0]-Population[0][PopulChromosCount-1])*0.01-Population[0][PopulChromosCount-1]; //---------------------------------------------------------------------- for(i=0;i<PopulChromosCount;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(Population[0][i]+delta); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[PopulChromosCount-1][1]); for(u=0;u<PopulChromosCount;u++) if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; return(u); } //————————————————————————————————————————————————————————————————————————
3.15. RemovalDuplicates.删除重复染色体
该函数用于删除种群中的重复染色体,剩余的唯一染色体(对于当代种群而言是唯一的)将按照由优化类型所决定的顺序(即递减或递增)由 VFF 存储。
//———————————————————————————————————————————————————————————————————————— //根据 VFF中的排序删除重复染色体 void RemovalDuplicates() { //-----------------------变量------------------------------------- int chromosomeUnique[1000];//保存每个染色体唯一特性的数组: // 0-重复, 1-唯一 ArrayInitialize(chromosomeUnique,1); //假定没有重复 double PopulationTemp[][1000]; ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Ge =0; //基因索引 int Ch =0; //染色体索引 int Ch2=0; //第二个染色体的索引 int cnt=0; //计数器 //---------------------------------------------------------------------- //----------------------删除重复染色体---------------------------1 //从一对中选择第一个做比较... for(Ch=0;Ch<PopulChromosCount;Ch++) { //如果不是重复的... if(chromosomeUnique[Ch]!=0) { //从一对中选择第二个... for(Ch2=0;Ch2<PopulChromosCount;Ch2++) { if(Ch!=Ch2 && chromosomeUnique[Ch2]!=0) { //相同基因计数器清零 cnt=0; //比较基因. 有相同基因出现 for(Ge=1;Ge<=GeneCount;Ge++) { if(Population[Ge][Ch]!=Population[Ge][Ch2]) break; else cnt++; } //如果相同基因数和总基因数相等 //..染色体会被认为是重复的 if(cnt==GeneCount) chromosomeUnique[Ch2]=0; } } } } //计算唯一染色体数量的计数器 cnt=0; //把唯一的染色体复制到临时数组中 for(Ch=0;Ch<PopulChromosCount;Ch++) { //如果染色体是唯一的就复制, 否则到下一个 if(chromosomeUnique[Ch]==1) { for(Ge=0;Ge<=GeneCount;Ge++) PopulationTemp[Ge][cnt]=Population[Ge][Ch]; cnt++; } } //给 "全部染色体"变量赋值为唯一染色体计数器的值 PopulChromosCount=cnt; //把唯一染色体返回到 //综合种群的临时存储数组 for(Ch=0;Ch<PopulChromosCount;Ch++) for(Ge=0;Ge<=GeneCount;Ge++) Population[Ge][Ch]=PopulationTemp[Ge][Ch]; //=================================================================1 //----------------种群排序---------------------------2 PopulationRanking(); //=================================================================2 } //————————————————————————————————————————————————————————————————————————
3.16. PopulationRanking.种群排序
排序由 VFF 完成。此方法类似于冒泡排序法(该算法重复地走访过要排序的数组。每次走访,依次将元素两两进行比较,如果元素对的顺序错误,则交换两个元素的位置。走访数组的工作将重复地进行,直到不再需要交换 - 也就是说该数组已完成排序。
在算法走访数组时,不在适当位置的元素“浮动”到所需位置,就像水中的气泡一样,这就是算法名字的由来,但有一点不同,参与排序的是数组的索引,而非数组的内容。相比简单地将数组复制到其他数组,此方法要更快,在速度上稍有差异。排序的数组越大,差异就越小。
//———————————————————————————————————————————————————————————————————————— //种群排序. void PopulationRanking() { //-----------------------变量------------------------------------- int cnt=1, i = 0, u = 0; double PopulationTemp[][1000]; //临时种群 ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Indexes[]; //染色体索引 ArrayResize (Indexes,PopulChromosCount); ArrayInitialize(Indexes,0); int t0=0; double ValueOnIndexes[]; //对应染色体索引的VFF // ArrayResize (ValueOnIndexes,PopulChromosCount); ArrayInitialize(ValueOnIndexes,0.0); double t1=0.0; //---------------------------------------------------------------------- //填充临时数组 temp2 的索引并且 //从排好顺序的数组中复制第一行 for(i=0;i<PopulChromosCount;i++) { Indexes[i] = i; ValueOnIndexes[i] = Population[0][i]; } if(OptimizeMethod==1) { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]>ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } else { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]<ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } //根据获得的索引建立排好序的数组 for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) PopulationTemp[i][u]=Population[i][Indexes[u]]; //把排好序的数组复制回来 for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) Population[i][u]=PopulationTemp[i][u]; } //————————————————————————————————————————————————————————————————————————
3.17. RNDfromCustomInterval.给定的区间的随机数发生器
一个方便的功能。在 UGA 中十分方便。
//———————————————————————————————————————————————————————————————————————— //在给定区间内的随机数发生器 double RNDfromCI(double RangeMinimum,double RangeMaximum) { return(RangeMinimum+((RangeMaximum-RangeMinimum)*MathRand()/32767.5));} //————————————————————————————————————————————————————————————————————————
3.18. SelectInDiscreteSpace.在离散空间中选择
用于减少搜索空间。如果参数 step = 0.0,搜索在连续空间中执行(受限于语言限制,在 MQL 中受限于第 15 个重要标志 inclusive)。 要使 GA 算法具有更高的精度,您需要编写额外的库以使用长数。
RoundMode = 1 时函数的工作可通过下图表示:
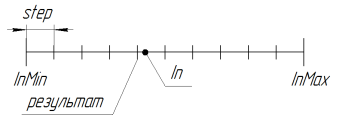
图 11. RoundMode = 1 时函数 SelectInDiscreteSpace 的工作
//———————————————————————————————————————————————————————————————————————— //在离散空间内选择. //模式: //1-下方最接近 //2-上方最接近 //任何最接近 double SelectInDiscreteSpace ( double In, double InMin, double InMax, double step, int RoundMode ) { if(step==0.0) return(In); // 保证边界正确性 if( InMax < InMin ) { double temp = InMax; InMax = InMin; InMin = temp; } // 在突破中 - 返回突破的边界 if( In < InMin ) return( InMin ); if( In > InMax ) return( InMax ); if( InMax == InMin || step <= 0.0 ) return( InMin ); // 带到指定的尺度中 step = (InMax - InMin) / MathCeil ( (InMax - InMin) / step ); switch( RoundMode ) { case 1: return( InMin + step * MathFloor ( ( In - InMin ) / step ) ); case 2: return( InMin + step * MathCeil ( ( In - InMin ) / step ) ); default: return( InMin + step * MathRound ( ( In - InMin ) / step ) ); } } //————————————————————————————————————————————————————————————————————————
3.19. FitnessFunction.适应度函数
该函数不是 GA 的一部分,它接收将为其计算 VFF 的种群中染色体的索引。VFF 被写入传递染色体的零索引。该函数的代码对每个任务而言都是唯一的。
3.20. ServiceFunction.服务函数
该函数不是 GA 的一部分,它的代码对每个特定任务而言都是唯一的。它可用于实施对代的控制。例如,为了显示当前代的最优 VFF。
我们将所有优化问题分为两类,它们都可以通过 EA 解决:
4.1. 例 1
我们来讨论答案已知的问题,以确保算法工作,然后继续解决问题,其算法是很多交易人员都感兴趣的。
问题:求函数 "Skin" 的最小值与最大值:
区间为 [-5, 5]。
答案:fmin (3.07021,3.315935) = -4.3182,fmax (-3.315699; -3.072485) = 14.0606。
图 12. "Skin" 在区间 [-5, 5] 上的图形
为解决此问题,我们编写了以下脚本:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" #include "Skin.mqh"//测试函数 //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------外来参数-------------------------------- input string GenofundParam = "----基因池参数----"; input int ChromosomeCount_P = 50; //群体中的染色体数 input int GeneCount_P = 2; //基因数 input int FFNormalizeDigits_P = 4; //适应度符号数 input int GeneNormalizeDigits_P = 4; //基因数 input int Epoch_P = 50; //无进展世代数 //--- input string GA_OperatorParam = "----算子参数----"; input double ReplicationPortion_P = 100.0; //复制比例. input double NMutationPortion_P = 10.0; //自然突变比例. input double ArtificialMutation_P = 10.0; //人工突变比例. input double GenoMergingPortion_P = 20.0; //借用基因比例. input double CrossingOverPortion_P = 20.0; //交叉比例. //--- input double ReplicationOffset_P = 0.5; //区间边界转换系数 input double NMutationProbability_P= 5.0; //每个基因突变可能性百分率 //--- input string OptimisationParam = "----优化参数----"; input double RangeMinimum_P = -5.0; //最小搜索范围 input double RangeMaximum_P = 5.0; //最大搜索范围 input double Precision_P = 0.0001;//所需的精确度 input int OptimizeMethod_P = 1; //优化方法:1-最小,其他-最大 //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------全局变量----------------------------- double ERROR=0.0;//基因中的平均错误 //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------程序主体-------------------------------- int OnStart() { //-----------------------变量------------------------------------- //准备 UGA 的全局变量 ChromosomeCount=ChromosomeCount_P; //群体中的染色体数 GeneCount =GeneCount_P; //基因数 RangeMinimum =RangeMinimum_P; //最小搜索范围 RangeMaximum =RangeMaximum_P; //最大搜索范围 Precision =Precision_P; //搜索步长 OptimizeMethod =OptimizeMethod_P; //1-最小, 其他 - 最大 FFNormalizeDigits = FFNormalizeDigits_P; //适应度小数点位数 GeneNormalizeDigits = GeneNormalizeDigits_P;//基因小数点位数 ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //无进展世代数 //---------------------------------------------------------------------- //局部变量 int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //运行 UGA 主函数 UGA ( ReplicationPortion_P, //复制比例. NMutationPortion_P, //自然突变比例. ArtificialMutation_P, //人工突变比例. GenoMergingPortion_P, //借用基因比例. CrossingOverPortion_P,//交叉比例. //--- ReplicationOffset_P, //区间边界转换系数 NMutationProbability_P//每个基因突变可能性百分率 ); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," mc - 实现时间"); //---------------------------------- return(0); } //————————————————————————————————————————————————————————————————————————
以上便是解决该问题的脚本的完整代码。运行程序,我们将得到函数 Comment () 提供的信息:
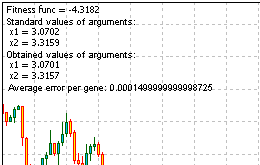
图 13. 解决问题的结果
查看结果,我们可以得出算法工作的结论。
4.2. 例 2
人们普遍认为,指标 ZZ 显示了转向交易系统的理想输入。该指标在“波动理论”的拥护者中很受欢迎,他们用它来确定“数据”的大小。
问题:在放弃更多理论增益点求和的情况下,确定转向交易系统在历史数据上是否有 ZZ 顶点以外的其他入口点?
针对该试验,我们为 M1 的 100 个柱选择 GBPJPY 对。接受 80 点差(五位数报价)。开始前,您需要确定最佳 ZZ 参数。为此,我们编写一段简单的脚本,通过简单枚举找出 ExtDepth 参数的最佳值:
#property script_show_inputs //———————————————————————————————————————————————————————————————————————— //----------------------外来参数-------------------------------- input int History=100; input double Spred =80.0; input int Depth =5; //为“一次性”使用 input bool loop =true;//是否使用枚举 //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------程序主体-------------------------------- void OnStart() { //-----------------------变量------------------------------------- double ZigzagBuffer [];//保存之字线指标缓冲区 double PeaksOfZigzag[];//保存之字线极值数值 int Zigzag_handle; //指标句柄 ArraySetAsSeries(ZigzagBuffer,true); ArrayResize(PeaksOfZigzag,History); int depth=3; double PipsSum=0.0; int PeaksCount=0; bool flag=true; //---------------------------------------------------------------------- if(loop==true) { while(depth<200 && flag==true) { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",depth); //--- 重置代码错误 ResetLastError(); //--- 尝试复制指标值 for(int i=0;i<100;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("无法复制指标缓冲区. 错误 =",GetLastError()," 复制数=",copied); return; } //----------------------------------------------------------- PipsSum=0.0; PeaksCount=0; for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; //----------------------------------------------------------- if(PeaksCount<=2) flag=false; else { Print(depth," ",PeaksCount," ",PipsSum); depth+=1; } //----------------------------------------------------------- } } else { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",Depth); //--- 重置错误编码 ResetLastError(); //--- 尝试复制指标值 for(int i=0;i<History;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("无法复制指标缓冲区. 错误 =",GetLastError()," 复制数=",copied); return; } //----------------------------------------------------------- for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; } Print(Depth," ",PeaksCount," ",PipsSum); //----------------------------------------------------------- } } //————————————————————————————————————————————————————————————————————————
通过运行脚本,我们获得 ExtDepth = 3 的 4077 个点。19 个指标顶点位于 100 个柱上。随着 ExtDepth 增大,ZZ 顶点的数目减少,盈利能力也降低。
现在,我们可以使用 UGA 找出替代 ZZ 的顶点。对于每个柱,ZZ 顶点可以有三个位置:1) 最高点,2) 最低点,3) 无顶点。顶点的存在和位置的信息将由每个柱的每个基因携带。因此,染色体的大小为 100 个基因。
根据我的计算(如果存在错误,请擅于数字计算的读者纠正),在 100 个柱上您可以建立 3 ^ 100 或 5.15378e47 个替代选项 "ZigZags"。这是使用直接枚举需要考虑的选项的确切数目。按照每秒钟 100000000 个项目的计算速度,我们将需要 1.6e32 年的时间来完成计算!这比宇宙存在的时间还要长。至此我开始怀疑是否能找到该问题的解决方案。
但我们还是要迈出这一步。
由于 UGA 使用实数表示染色体,我们需要以某种方式对顶点的位置进行编码。这正是染色体的基因型与表型不匹配的情形。为基因分配搜索区间 [0, 5]。我们约定,区间 [0, 1] 对应于 ZZ 的顶点位于最高点,区间 [4, 5] 对应于顶点位于最低点,而区间 [ 1, 4 ] 对应于顶点缺失。
我们需要考虑一个重要的点。由于原型种群是使用基因在指定区间中随机生成,第一个样本将具有极差的结果,甚至可能有几百个点带有负号。在经过数代后(虽然也有在第一代发生的几率),我们将看到其基因大体上与顶点缺失相一致的样本出现。这意味着没有交易和不可避免的点差的补偿。
根据一些前交易人员的说法:“交易的最佳策略是不要交易”。此个体将作为人工进化的顶点。为了使该“人工”进化产生交易个体,即令其排列替代 ZZ 的顶点,我们分配个体适应度、缺失的顶点、值 "-10000000.0",有意将其放置在相比任何其他个体的进化的最底层。
下面是使用 UGA 寻找替代 ZZ 的顶点的脚本代码:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------外来参数-------------------------------- input string GenofundParam = "----基因池参数----"; input int ChromosomeCount_P = 100; //群体中的染色体数 input int GeneCount_P = 100; //基因数 input int FFNormalizeDigits_P = 0; //适应度小数点位数 input int GeneNormalizeDigits_P= 0; //基因小数点位数 input int Epoch_P = 50; //无进展世代数 //--- input string GA_OperatorParam = "----算子参数----"; input double ReplicationPortion_P = 100.0; //复制比例. input double NMutationPortion_P = 10.0; //自然突变比例. input double ArtificialMutation_P = 10.0; //人工突变比例. input double GenoMergingPortion_P = 20.0; //借用基因比例. input double CrossingOverPortion_P = 20.0; //交叉比例. input double ReplicationOffset_P = 0.5; //区间转换系数 input double NMutationProbability_P= 5.0; //每个基因突变可能性百分率 //--- input string OptimisationParam = "----优化参数----"; input double RangeMinimum_P = 0.0; //最小搜索范围 input double RangeMaximum_P = 5.0; //最大搜索范围 input double Precision_P = 1.0; //请求的精确度 input int OptimizeMethod_P = 2; //优化方法:1-最小,其他 -最大 input string Other = "----其他----"; input double Spred = 80.0; input bool Show = true; //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------全局变量----------------------------- double Hight []; double Low []; datetime Time []; datetime Ti []; double Peaks []; bool show; //———————————————————————————————————————————————————————————————————————— //--------------------------程序主体-------------------------------- int OnStart() { //-----------------------变量------------------------------------- //为UGA准备全局变量 ChromosomeCount=ChromosomeCount_P; //群体中的染色体数 GeneCount =GeneCount_P; //基因数 RangeMinimum =RangeMinimum_P; //最小搜索范围 RangeMaximum =RangeMaximum_P; //最大搜索范围 Precision =Precision_P; //搜索步长 OptimizeMethod =OptimizeMethod_P; //1-最小, 其他 - 最大 FFNormalizeDigits = FFNormalizeDigits_P; //适应度小数点位数 GeneNormalizeDigits = GeneNormalizeDigits_P;//基因小数点位数 ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //无进展世代数 //---------------------------------------------------------------------- //准备全局变量 ArraySetAsSeries(Hight,true); CopyHigh (NULL,0,0,GeneCount+1,Hight); ArraySetAsSeries(Low,true); CopyLow (NULL,0,0,GeneCount+1,Low); ArraySetAsSeries(Time,true); CopyTime (NULL,0,0,GeneCount+1,Time); ArrayResize (Ti,GeneCount+1);ArrayInitialize(Ti,0); ArrayResize(Peaks,GeneCount+1);ArrayInitialize(Peaks,0.0); show=Show; //---------------------------------------------------------------------- //局部变量 int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //删除对象并重画图表 ObjectsDeleteAll(0,-1,-1); ChartRedraw(0); //运行UGA主函数 UGA ( ReplicationPortion_P, //复制比例. NMutationPortion_P, //自然突变复制比例. ArtificialMutation_P, //人工突变比例. GenoMergingPortion_P, //借用基因比例. CrossingOverPortion_P,//交叉比例. //--- ReplicationOffset_P, //区间边界转换系数 NMutationProbability_P//每个基因突变可能性百分率 ); //---------------------------------- //在屏幕上显示最后结果 show=true; ServiceFunction(); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," мс - 执行时间"); //---------------------------------- return(0); } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // 服务函数. 从 UGA 中调用. | | //如果不需要它,把函数设空, 如下: | // 无效 ServiceFunction() | // { | // } | //-----------------------------------------------------------------------+ void ServiceFunction() { if(show==true) { //-----------------------变量----------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //-------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Chromosome[u]; if(temp<=1.0 ) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } } ObjectsDeleteAll(0,-1,-1); for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; ObjectCreate (0,"BoxBackName"+(string)V,OBJ_TREND,0,Ti[V],Peaks[V],Ti[V+1],Peaks[V+1]); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_COLOR,Black); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_SELECTABLE,true); } ChartRedraw(0); Comment(PipsSum); } //---------------------------------------------------------------------- else return; } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // 确定个体适应度的函数从 UGA 中调用. | //-----------------------------------------------------------------------+ void FitnessFunction(int chromos) { //-----------------------变量------------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //---------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Colony[u][chromos]; if(temp<=1.0) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); PeaksCount++; } } if(PeaksCount>1) { for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; Colony[0][chromos]=PipsSum; } else Colony[0][chromos]=-10000000.0; AmountStartsFF++; } //————————————————————————————————————————————————————————————————————————
运行脚本后,我们得到总盈利为 4939 点的顶点。此外,相比采用直接枚举所需的 3 ^ 100 次操作,它仅使用了 17,929 次计算。在我的电脑上,这就是 21.7 秒和 1.6e32 年的对比!
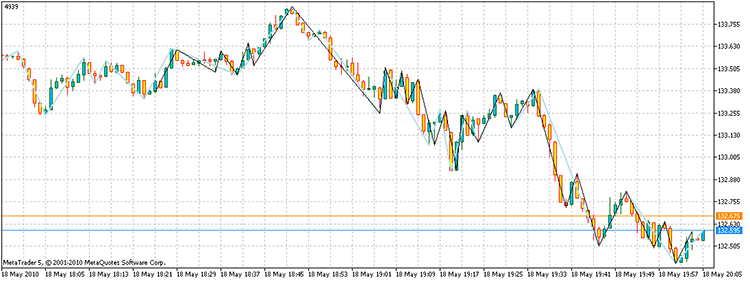
图 14. 问题解决方案的结果。黑色线段 - 替代 ZZ,天蓝色 - ZZ 指标
因此,问题的答案为:“存在其他入口点”。
结合功能十分强大的人员配置终端策略测试程序,MQL5 语言允许您为交易人员创建功能毫不逊色的工具,并使您能够解决真正复杂的问题。我们获得了一个十分灵活且扩展性良好的优化算法。我无法掩饰对这一发现的骄傲感和自豪感,虽然我并不是它的始创者。
由于 UGA 最初是以这样的一种方式设计,它可以很容易地修改并使用其他算子和运算块进行扩展,读者将能够轻松地为“人工”进化的开发添砖加瓦。
我祝愿读者成功找到最优解,并希望在此过程中能略尽绵薄之力。祝您好运!
注意: 本文使用了指标 ZigZag。UGA 的所有源代码已附于本文。
许可: 附于本文的源代码(UGA 代码)在 BSD 授权条件下传播。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
