掷硬币游戏很久以来就存在了。让我们来玩这个游戏,不过目的在于测试并理解 FOREX 市场中的技术交易机制。我们并不是第一个将硬币拿在手中的人。那些希望更加详细地学习概率论的人可以参考 William Feller 所写的《An Introduction to Probability Theory and Its Applications》(概率论及其应用)一书。我们的目标是理解交易机制。
我们先使用随机数生成器模拟掷硬币游戏的结果。那么,让正面为 +1,反面为 -1。第 i 次掷硬币的结果为 x (i) = p (1/2),其中 p (1/2) 为一个函数,取值为 +1,其概率为 1/2 以及 -1,其概率同样为 1/2。
则随机游走将只是 x(i) 的和。为了简化,我们从零开始。
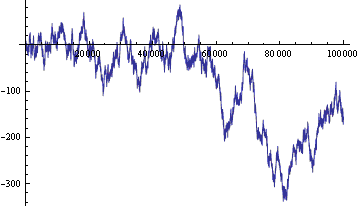
图 1. 随机游走:(垂直轴 - 线条上的当前位置,水平轴 - 时间步数)
随机游走经过充分的研究,并且具有某些显著的特性。让我们总结一下对我们有用的特性:
随机游走可用于交易。实际上,长久以来,学生们已经注意到这种现象,并且在课间休息时玩“正面或反面”的游戏。随机游走可用于组织一个赌博市场。当前市场中的所有交易规则都适用,但是代替采有货币汇率,我们采用随机游走汇率。同平常一样,将有一些收取点差、手续费和税费的中间人。但是我们将善意地请求他们从现在起不要拿走任何东西了,并且不要破坏我们的游戏。
关于交易的一些解释:
真实货币报价和随机游走数据之间的差异
第 1-8 条说法非常悲观。它们预测在随机游走市场中交易的任何交易者都会无条件损失预付款。但是货币对的报价不同于随机游走数据。这些差异是制定一个可盈利(平均而言)的交易策略的关键。让我们列出真实货币汇率和随机游走数据之间的主要差异。
随机游走中的众多变化是一系列的随机取值 +1 和 -1。那么,我们如何在这个序列中找到统计趋势?此问题与验证序列是否具有随机性的任务一致。已经开发出很多随机性测试。如果任何测试在一个序列中显示出“随机性”,则可以据其制定交易策略。
趋势的概念
最简单的测试如下所述。一个序列中 +1 和 -1 的数量大体是相同的。按照醉酒水手理论,一般而言,+1 的数量与 -1 的数量之差不会超过序列中数据数量的平方根。对于实际汇率,通过基础通道对真实汇率施加的限制来执行此随机性测试。在这里,我们不能制定一个交易策略。
另一测试要有趣得多。让我们统计 "+1,+1"、"+1,-1"、"-1,+1" 和 "-1,-1" 链的数量。在一个随机序列中,各个数字的数量应大体相同(再一次指出,类似于醉酒水手理论)。如果 "++" 链(重命名为 "+1+1")的数量突然远大于 "+-" ("+1,-1") 链的数量,则我们制定一个策略:在每个 "+" 之后,我们下注于 "+"。依据统计,我们应该有一半以上的赢钱可能。
让我们将最后一段转换为交易者的语言。最流行的交易策略为顺势策略。及时辨别趋势,从而及时进入或退出是这些策略的主要目的。但存在错误的趋势幻想,如同随机游走。上述链的数量测试,将有助于从真实趋势中区分出错误趋势。如果 "++" 和 "--" 链的数量大于 "+-" 和 "-+" 的数量,则随机游走具有趋势,并且顺势策略将起作用。如果不是,则我们不应依据基于顺势策略的信号进入市场。
我们可以不仅仅考虑二项链 (++,+-,-+,--),还可以考虑三项链 (+++, ++-, +-+, ...),甚至更长的链。我们可以统计顺势 (+++, ---, ++++) 和逆势 (-+-, +-+, +-+-) 链的数量,或者向每个链赋予一个趋势系数并使用系数计算和值。最终,这些步骤将让我们得出 Z 分的计分。但是在这里,Z 分并不是按交易者习惯的一系列赢-输策略计算的,而是按汇率改变计算的。负的 Z 分表示序列有趋势,而正的 Z 分表示序列无趋势。
长链的考虑和 Z 分的计算需要足够长的序列(从 30 个元素起)。我们的目的是构建趋势指标,而考虑长序列将导致指标的延迟。二项链的考虑可从 8 个元素的序列开始。因此,为了构建指标,让我们考虑二项链。为了认真研究随机游走(比如构建随机游走模拟程序),我们需要使用 Z 分。
随机游走中趋势的说明
让我们说明随机游走中的趋势概念。
趋势的一个定义如下:趋势 - 以前变化的记忆。随机游走不会记住其历史。让我们向其添加记忆,让第 i 次掷硬币的结果为 x (i) = p(1/2 + a*x(i-1)),其中 a 是介于 -1/2 和 +1/2 之间的顺势参数。函数 P (...) 在 1/2+a*x(i-1) 的概率时值为 +1,在 1/2-a* x(i-1) 的概率时值为 -1。
如果 а<0,则随机游走是逆势。如果 а>0,则随机游走是趋势。如果 а=0,则随机游走没有趋势。
下图显示了以相同序列的随机数字生成的随机游走。
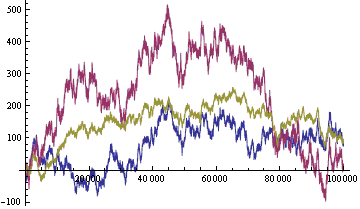
图 2. 生成的随机游走:顺势(红色,a = 0.2),无趋势(蓝色,a = 0),逆势(黄色,a =- 0.2)
如我们所见,顺势随机游走的特征为相对较高的波动,形成下降通道的趋势。逆势随机游走具有相对较低的波动,形成在一个水平通道中卷起的趋势。
在实际市场中,顺势和逆势随机游走的区别并不是如此简单,尤其是在趋势很弱时。趋势指标绝对是至关重要的。如前文所述,在无趋势和逆势随机游走情况下使用顺势策略肯定会导致预付款的损失。
在顺势随机游走情况下,您可以使用顺势策略进行交易。趋势捕捉和趋势反转点的检查可由数学统计方法来代替。但是问题仍然存在:是否有足够的非随机盈利来支付中间人费用并仍然保持盈利?为了获得近似的答案,我们将不得不转到在本文的末尾提供的趋势指标。
在逆势随机游走情况下,我们可以波段交易。逆势随机游走旨在打破任何陡峭的趋势并移到水平通道。您可以在水平通道的任何位置设置获利点,无论当前趋势如何,以及在通道边界之外设置止损点。无论价格在通道的哪个地方徘徊,最终都将触碰获利点。
在无趋势随机游走情况下,我们不能采用顺势策略进行交易。我们需要采用其他理念,例如循环。
针对随机游走模拟程序的建议
有趋势的随机游走对测试交易策略也有用。我们可以依据以下函数创建随机游走模拟程序:
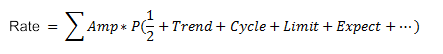
其中:
这些函数的参数被调整到真实汇率的统计参数。
通过随机游走来模拟真实汇率比人类感知的缺点的说明有更深的含义。用随机游走来模拟汇率数据允许您依据可能的完整汇率集合(或至少依据完整集合的合理样本)来测试任何 EA 交易。这样又允许我们依照给定的 EA 交易构建概率分布函数。此分布函数以特有的方式指出 EA 的盈利能力、进取性和其他参数的特征。
集合完整性的定义:
对历史数据进行测试总比没有的好。但是缺少历史数据并且它已经过时了。此外,历史数据可能以优化的形式包含在 EA 的设计中 - 那么我们如何测试它们呢?因此,EA 以历史数据为基础的资产净值曲线只是以历史上曾经出现过的汇率实施为基础的资产净值的概率分布函数的一部分。并且它并不足以完整地描述 EA 交易的特征。
当然,我们绝对不可能在模拟汇率中采用实际汇率的所有细节和细微差别。实际汇率的模拟会在其他文章和研究中单独地进行深入讨论。但首先要测试顺势系统,我们可以依据有趋势的随机游走使用相当简单的模拟程序。
只需要将一个能够确定分布函数的简单模拟程序连接到策略测试程序。需要模拟程序的另一个地方是销售 EA 的店面。否则我们将发现难以看到我们正在购买的是什么。我只会在对几个根本上不同的模拟程序和历史数据测试之后才会购买交易 EA。对于每个正在销售的 EA,除了价格以外,还应有附带的资金概率分布函数以及从中得出分布函数的模拟程序。
EA 交易的概率分布函数是生产者提供的 EA 技术通行证和保证。俄罗斯联邦的消费者权益保护法适用于 EA,如同适用于任何其他产品一样。然而,在这里,我们首先需要为模拟程序构建一个认证系统。
趋势指标
使用汇率趋势这一理念,我们能够构建最简单的趋势指标。与随机游走不同,以柱来表示实际汇率。让我们用随机游走汇率来代替实际汇率。每根柱被单一的平均值(最高价 + 最低价)/ 2 代替(参见本文末尾的问题)。让我们抛开变化幅度不管,仅留下符号。我们获得一系列的加号和头号,例如 ++-+---+-+-- ....统计最后 N 根柱中 "++" 和 "--" 顺势链的数量以及 "+-" 和 "-+" 逆势链的数量。我们采取 "++" + "--" - "-+" - "+-" 的值作为一个指标。
为方便起见,让我们在指标上画一条线,该线将评估趋势的强度:+ 或 - N 的平方根。
在本文的末尾提供了以 MQL5 语言编写的指标代码 (TrendingHL.mq5)。
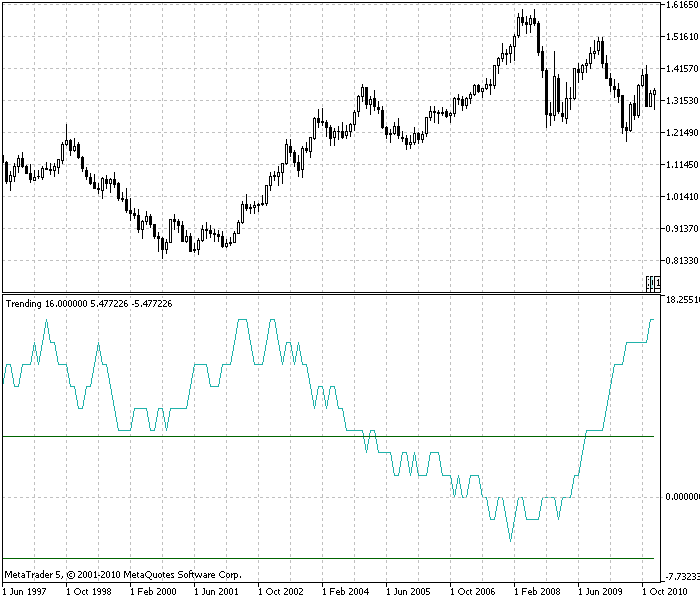
图 3. EURUSD 趋势指标,时间框架为每月。汇率几乎始终是顺势(在零线上方),一半的时间是强趋势(高于上方的绿线)。据其评估趋势的柱的数量 N=30
在查看 EURUSD 汇率的趋势指标之后,我们注意到:
指标在大多数时间大于零。即汇率是顺势的。已经讨论过弱的汇率趋势。但是图形值得详细讨论。
实际汇率并不始终都是顺势的。
趋势指标和其他指标一样,都是有延迟的。
趋势指标允许我们估计可通过此图表上的顺势交易策略获得的非随机盈利的大小。图表指标的平均值约等于 7。一根柱的汇率平均变化为 0.01 美元(近似值)。0.01*7=0.07. 因此,每投资一美元,我们每月大约可赚 7 美分的利润。这是一个大概估计,但是向我们提供了一个量级。我们忽略了中间人、预付款交易、市场的进入点和退出点。
好消息是,与随机游走汇率不同,实际汇率是顺势的,让我们赚钱。
令人冷静的事实是,与其他投资工具相比,资本产生的利息非常低。
就多年以来的平均值而言,趋势是正的这一事实使指标具备预测能力。我们能够希望汇率的顺势性仍然继续。
在大的时间框架内最能看到趋势。
很少看到逆势。
尽管实际汇率是不规则的,却不能将比例(时间框架)变化下的趋势不变性概念与确定性联系在一起。
以下可能是一个正确的假设:相对盈利在比例变化下是不变的。
![]()
其中:
同时,各种真实汇率及各种投资工具的盈利得以保留——不仅仅是在不同的时间框架中,也在不同的交易理念中(周期、波动)。在上方,盈利能力受到大量投机者和投资者的限制。在下方,所有工具的总盈利受到总资金量的增加的限制,或者概而言之:受到人类发展的限制。
依据最后一段,我们可以构建一个汇率的顺势盈利指标,并且涉及其他理念和一个指标(总盈利)。通过为其他工具构建类似的指标,我们将开始研究整个市场的资本流动,然后我们便可能更加精确地预测汇率。
让我更加详细地解释最后一段。对汇率有两种预测:
我们按指标统计的 7% 的顺势盈利能力(参见“非随机趋势”)是上述两个非随机性以及某些我尚不知道的非随机性的总和。
在这里,市场被视为具有流入和流出的非封闭式(开放式)系统。增加 = 流入 - 流出。如果流入大于流出,则市场(市场汇率)是顺势。如果流入等于流出,则市场无趋势。如果流入小于流出,则市场是逆势。
本文有一个严重的矛盾之处。一方面,我们使用趋势指标确立实际汇率是顺势的结论。但是另一方面,我们认为实际汇率在一个水平基础通道的限制内波动。而水平通道是逆势的一个极度明显信号。
那么,实际汇率究竟是顺势还是逆势?一种和谐感让我认为实际汇率是顺势,没有水平基础通道存在。这意味着历史上的最高价和最低价将不断变化。与之相对应,危机将越来越强,直到下一个危机摧毁系统。一般而言,这是能够被理解的,趋势是系统中某些参数(资产净值)正在累积的信号,它增加了。如果我们持续加载系统,它最终会崩溃。累积参数将重置,新的发展周期开始。
总结
这是另一篇关于 FOREX 市场的文章。可以在互联网中找到数以百计这样的文章,平均每篇一美元。免费文章则无以计数。那么,这篇文章中有何新意呢?
问题:为什么要对指标取平均值(最高价 + 最低价)/2?考虑到我们不能以此价格进行交易。取平均值是危险的 - 平均(光滑)随机游走汇率将有趋势。此外,给出的平均值(光滑值)越多,趋势将越强。
回答:让我们进行检查。要对此进行检查,我们可以采用没有进行任何平均化的价格,例如开盘价或收盘价 - 趋势将仍然存在,但是也看不见)。
让我们考虑一下趋势指标(EURUSD,每月时间框架)取平均值的效果。下面的指标是依据平均值(最高价 + 最低价)/2 计算的 (trendinghl.mq5)。中间的指标是依据开盘价计算的 (trendingopen.mq5)。上面的指标是依据收盘价计算的 (Trendingclose.mq5)。显然所有指标都是正的,并且汇率有趋势。但是开盘价指标和收盘价指标的平均值不等于 7,而是约等于 2,尽管(最高价 + 最低价)/2 指标的平均值等于 7。对于本文用来提供估值的精确度而言,该差异无关紧要。我必须承认取平均值人为地增大了汇率的趋势。
可以使用以下关键字通过搜索找到有关汇率趋势的更多引人满目的、精确的、权威的和具有挑战性的证据(测量结果):趋势、持续性、赫斯特指数 ... .
问题的一部分,“我们毕竟不能在此价格交易”是不切实际的认识。反对者期待(并且潜意识地寻求)该指标,通过该指标,他能亲眼看到信号并亲手知情地交易。我不得不让你失望了。计算机扼杀了人工交易。
如本文所评估,汇率的非随机性占每年资本的 10%(精确到量级)。此汇率值不可能被肉眼看到并抓牢。需要自动化 EA 交易。EA 将为一年中资本的几个百分点收益而战,并且在不久的将来,通过千分之一个百分点来进行。这是为什么我们需要一个模拟程序来跟踪和优化盈利百分比的几分之一的原因。
对实际汇率进行测试时,不可能检测到每年盈利小于 1% 的部分甚至是 1 个百分点。
这是为什么对模拟程序的数学引擎有非常高的要求的原因。
//+------------------------------------------------------------------+ //| Trending.mq5 | //| Copyright 2010, Grebenev V. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, Grebenev V." #property description "Trending Indicator" #property version "1.00" #property indicator_separate_window #property indicator_separate_window #property indicator_buffers 3 #property indicator_plots 3 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_SECTION #property indicator_type3 DRAW_SECTION #property indicator_color1 LightSeaGreen #property indicator_color2 DarkGreen #property indicator_color3 DarkGreen #property indicator_label1 "Trending" //--- input parameters N – number of bars, by which the trend is calculated input int N=30; double ExtTRbuffer[]; // array for the indicator double ExtTRbufferP[]; // array for the upper estimation of the trend double ExtTRbufferM[]; // array for the lower estimation of the trend double average[150000]; // array for the average values of the rates //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator digits // IndicatorSetInteger(INDICATOR_DIGITS,0); //--- indicator short name IndicatorSetString(INDICATOR_SHORTNAME,"Trending"); //---- index buffer SetIndexBuffer(0,ExtTRbuffer); SetIndexBuffer(1,ExtTRbufferP); SetIndexBuffer(2,ExtTRbufferM); //--- set index draw begin PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,1); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,1); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,1); //---- Array Initialization ArrayInitialize(ExtTRbuffer,0); ArrayInitialize(ExtTRbufferP,0); ArrayInitialize(ExtTRbufferM,0); ArrayInitialize(average,0); return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { double pp=0,pm=0,mp=0,mm=0; // pp - number of «++» chains, pm - number of «+-», mp – «-+», mm – «- -» / Fill the array of the average values of the rate with average values (high+low) /2 for(int i=prev_calculated;i<rates_total;i++) average[i]=(high[i]+low[i])/2; for(int i=prev_calculated;i<rates_total;i++) { pp=0; pm=0; mp=0; mm=0; for(int j=0;j<N;j++) { if(i-j-2>=0) // check that the index of the array did not exceed the border 0 { if((average[i-j-1]-average[i-j-2])>0 && (average[i-j]-average[i-j-1])>0) pp++; if((average[i-j-1]-average[i-j-2])>0 && (average[i-j]-average[i-j-1])<0) pm++; if((average[i-j-1]-average[i-j-2])<0 && (average[i-j]-average[i-j-1])>0) mp++; if((average[i-j-1]-average[i-j-2])<0 && (average[i-j]-average[i-j-1])<0) mm++; // chain containing "0" omitted } } // fill indicator arrays ExtTRbuffer[i]=pp+mm-pm-mp; ExtTRbufferP[i]=sqrt(N); ExtTRbufferM[i]=-sqrt(N); } return(rates_total); }

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
