概论
定义市场动态是交易者的主要任务之一。使用标准的技术分析工具来解决它往往太困难了。例如, МА 或 MACD 可能指引趋势, 但是我们仍然需要额外的工具来评估其动力和可靠性。最终, 它也许只是短线飙升, 然后迅速消退。
您可能知道这句至理名言: 为了外汇交易成功, 我们需要比其它市场参与者了解地更多。在此情况下, 您能够领先一步, 选择最有利的入场点, 并确保交易的可盈利性。成功的交易是若干优势的结合, 包括在趋势逆转, 或者巧妙利用基本面和技术数据, 以及情绪完全失控情况下准确地下单。所有这些都是交易事业成功的关键要素。
分形分析 也许会为许多市场评估问题提供全面的解决方案。分形往往被交易者和投资者所忽视, 尽管时间序列的分形分析可以有效地评估行情趋势及其可靠性。赫斯特 指数 是分形分析的基础数值之一。
在进入计算之前, 我们来简单地考察分形分析的主要规定, 并仔细观察赫斯特指数。
1. 分形行情假说 (FMH)。分形分析
分形 是具有自相似性的数学集合。一个自相似的对象与其自身的一部分完全或大致相似 (即整体具有与一个或多个部分相同的形状)。最生动的分形结构示例就是 "分形树":

自相似对象在不同的尺度上保持统计学上的相似性 — 空间或时间。
当应用于行情时, "f分形" 意味着 "反复性" 或是 "周期性"。
分形维度 定义对象或过程如何填充空间, 以及其结构在各种尺度上如何变化。当将此定义应用于金融 (或在我们的例子 — 外汇) 市场时, 我们可以说分形维数定义了时间序列的 "不规则性" (变异性) 的程度。相应地, 一条直线的 d 维度等于1, 随机散布 — d=1.5, 而在分形时间序列的情况下 1<d<1.5 或 1.5<d<1。
"FMH 的目的是给出适合我们观察的投资者行为和市场价格走势模型... 在任何时间, 价格也许不会反映出所有可用的信息, 而只能反映出对该投资期望重要的信息" — E. Peters, 分形行情分析。
我们不会详细介绍分形的概念, 并假设我们的读者已经对此分析方法有所了解。其应用于金融市场的综合描述可在 B. Mandelbrot 和 R. Hudson 所著的 "市场 (不当) 行为。金融湍流的分形视图", 以及 E. Peters 所著的 "分形行情分析" 和 "资本市场的混乱与秩序: 周期, 价格和市场波动的新视角" 等文章里找到。
2. R/S 分析法和赫斯特指数
2.1. R/S 分析法
分形分析的关键参数是研究时间序列的赫斯特指数。时间序列中两个相似值对之间的延迟越大, 赫斯特指数越小。
此指数是由 Harold Edwin Hurst - 哈罗德·埃德温·赫斯特 引入的 — 一位杰出的英国水文学家, 曾参与尼罗河大坝工程。为了着手施工, 赫斯特需要评估水位的波动。最初, 假设水流是随机注入的, 随机过程。然而, 赫斯特在研究了尼罗河九个世纪的洪水记录的同时, 设法总结出了这种范式。这是研究的起点。事实证明, 高于平均水平的洪灾随后会有更强劲的。之后, 这个过程改变其方向, 低于平均水平会紧随更弱的。这些显然是非周期性的轮回。
赫斯特的统计模型是基于阿尔伯特·爱因斯坦关于布朗运动的工作, 提供了粒子的随机散布模型。这个理论背后的思路是, 粒子走过的距离 (R) 与时间 (T) 的平方根成比例增加:
![]()
我们来改写一下等式: 在大量测试的情况下, 变化范围 (R) 等于测试次数 (T) 的平方根。赫斯特使用这个方程证明尼罗河洪水不是随机的。
为了形成他的方法, 水文学家使用了河流洪水的 X1..Xn 时间序列。稍后应用以下称为 重标极差法 或 R/S 分析法 的算法:
- 计算 X1..Xn 序列的平均值 Xm
- 计算序列标准偏差, S
- 从每个数值中扣除平均值 Zr (其中 r=1..n) 来对序列进行规范化
- 创建累积时间序列 Y1=Z1+Zr, 其中 r=2..n
- 计算累积时间序列的量级 R=max(Y1..Yn)-min(Y1..Yn)
- 将累积时间序列的量级除以标准偏差 (S)。
赫斯特扩展了爱因斯坦的方程, 将其转化为更常用的形式:
![]()
此处 c 是一个常数。
通常, R/S 值根据依赖度 H 即 赫斯特指数 随着时间增量的增加而改变尺度。
根据赫斯特, 如果洪水过程是随机的, H 将等于 0.5。然而, 在他的观察中, 他发现 H=0.91!这意味着规范化的量级比时间的平方根变化更快。换言之, 系统经过了一段比随机过程更长的距离, 这意味着过去的事件对当前和未来的事件都有重大影响。
2.2. 将理论应用到市场
随后, 赫斯特指数计算方法被适用到金融和股票市场。它包括将数据规范化为零平均值和单一的标准偏差, 以补偿通胀成分。换言之, 我们再次运用 R/S 分析法。
如何解释市场上的赫斯特指数?1. 如果赫斯特指数在 0.5 和 1 之间, 且它与期望值的差有两个及以上标准偏差, 则该过程符合长线记忆。换言之, 它有 持久性。
这意味着所有以下结果强烈依赖一段时间内的前一结果。最可靠及最有影响力的公司报价图表是最具说明性的 持久时间序列。美国公司诸如苹果, 通用电气, 波音, 以及俄罗斯的石油公司, 国际航空和外贸银行等都名列其中。这些公司的报价图表显示如下。我相信, 每位投资者都可以在观看这张图表的同时辨别一张熟悉的图片 — 每个新的最高价和最低价均高于前一根。
俄罗斯国际航空股票价格:
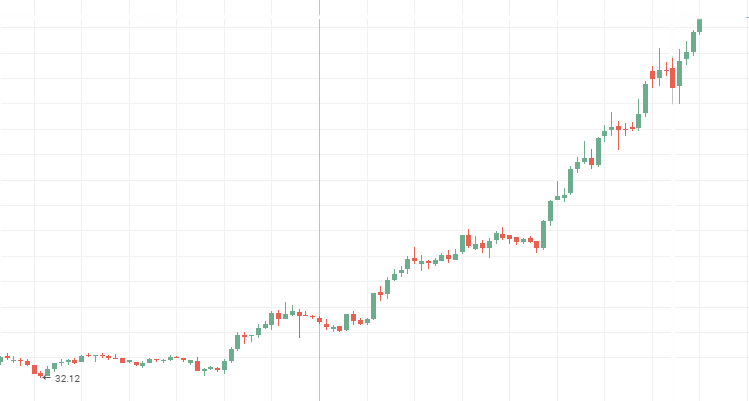
俄罗斯石油公司股票价格:
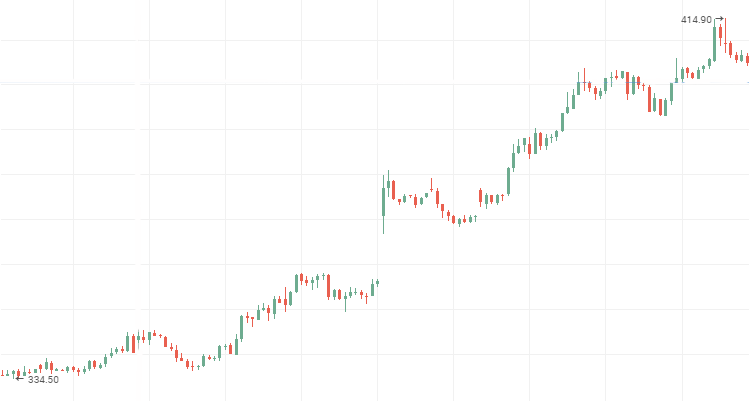
俄罗斯外贸银行股票价格, 下跌 持久性时间序列
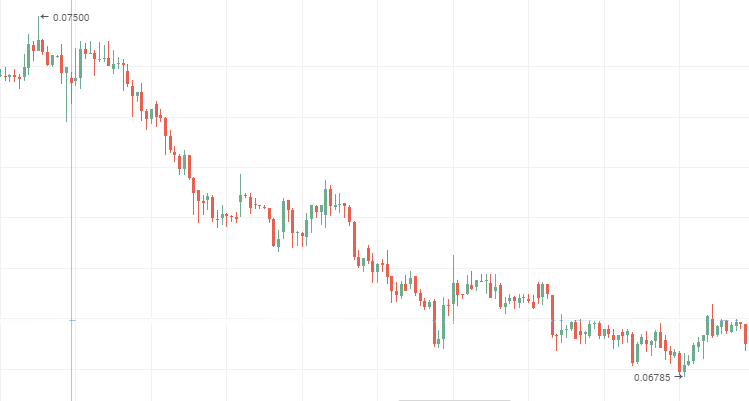
2. 如果赫斯特指数与预期值的两个或多个标准偏差的绝对差值在 0 和 0.5 之间, 这意味着我们正在处理 反持久性时间序列。
系统的变化比随机的变化更快, 即容易发生小而频繁的变化。反持久性 过程可以在二级股票图表中清晰看到。在横盘走势期间, "蓝筹" 价格图标也显示出反持续性行为。下面提供的 Mechel, AvtoVAZ 和 Lenenergo 的股票图表即是生动的 反持续性时间序列的例子。
Mechel 优先股:
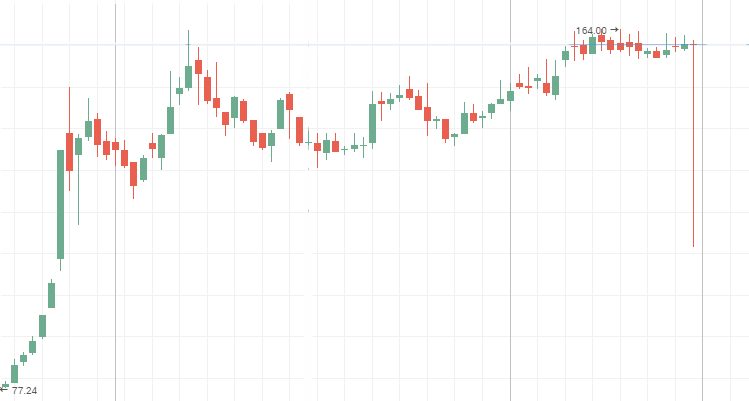
AvtoVAZ 普通股的一个横盘期间
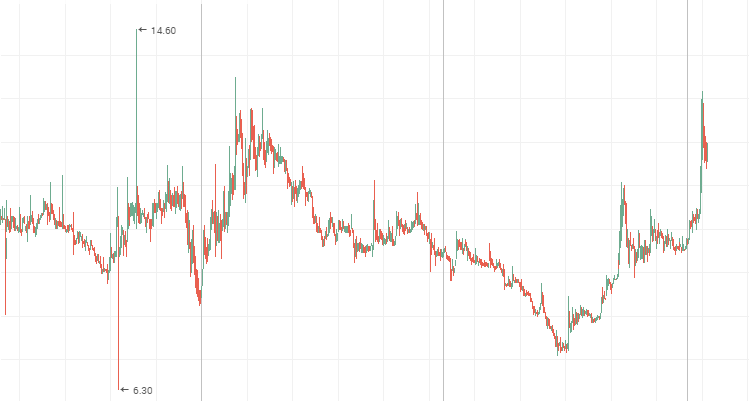
Lenenergo:
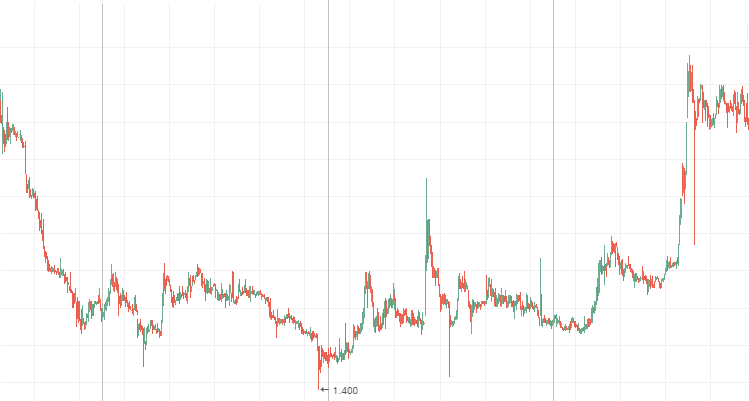
3. 如果赫斯特指数为 0.5 或者其值与期望值的差小于两个标准偏差, 则该过程被认定为随机游走。不要有短线或长线的周期性预期。在交易中, 这意味着技术分析没有什么帮助, 因为目前的价值几乎不受前市的影响。所以最好使用基本面分析。
股票市场工具 (各种公司, 工业公司和商品的证券) 的赫斯特指数样本如以下表格所示。针对过去 7 年进行计算。在 "金融危机" 期间, "蓝筹股" 指数下跌幅度较小。有趣的是, 许多二级证券表现出持久性, 证明其抗危机的稳健性。
| 名称 | 赫斯特指数, H |
|---|---|
| Gazprom |
0.552 |
| VTB |
0.577 |
| Magnit |
0.554 |
| MTS |
0.543 |
| Rosneft |
0.648 |
| Aeroflot | 0.624 |
| Apple | 0.525 |
| GE | 0.533 |
| Boeing | 0.548 |
| Rosseti |
0.650 |
| Raspadskaya |
0.656 |
| TGC-1 |
0.641 |
| Tattelecom |
0.582 |
| Lenenergo |
0.642 |
| Mechel |
0.635 |
| AvtoVAZ |
0.574 |
| Petrol | 0.586 |
| Tin | 0.565 |
| Palladium | 0.564 |
| Natural gas | 0.560 |
| Nickel | 0.580 |
3. 定义周期。分形分析中的记忆
我们如何确定自己的结果不是随机的 (微不足道的) ?为了回答这个问题, 我们应该首先研究 RS 分析, 假设分析系统是随机性质的。换言之, 我们应该检查空假设的有效性, 说明该过程是一个随机游走, 其结构是独立的且是正态分布的。
3.1. 计算期望的 R/S 分析值
我们来引入一个 期望的 R/S 分析值 概念。
在 1976 年, Anis 和 Lloyd 推导出一个表达必要预期值的方程式:
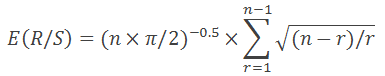
其中 n 是一定数量的观察值, 而 r 表示从 1 到 n-1 的整数。
如同在 "分形行情分析" 中所述, 提供的方程式仅对 n>20 有效。对于 n<20, 使用以下方程:
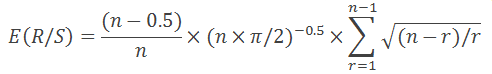
一切都很简单:
- 计算每个观测值的预期值, 并显示从 Log(N) 结合 Log(R/S) 的 Log(E(R/S)) 图示;
- 使用统计学理论中众所周知的方程式计算赫斯特指数的预期发散
![]()
此处 H 是赫斯特指数;
N – 样本中的观察数;
3. 通过评估 H 超过 E(H) 的标准偏差的数量来检查所获得的赫斯特比率的相关性。如果相关性绝对值超过 2, 则结果被认定是相关的。
3.2. 定义周期
我们来考虑下面的例子。绘制 RS 统计和预期值 E(R/S) 的两个图表, 并将其与市场动态进行比较, 以便了解计算结果是否符合报价走势。
Peters 指出, 定义循环存在的最佳方式是以对数建立一个 V 型统计图, 对数标尺基于一个子群中一定数量观察值的对数。
很容易评估得到的结果:
- 如果对数标尺图表是两轴上的水平线, 那么我们正在处理一个独立的随机过程;
- 如果图形具有正向上倾角, 我们正在处理一个持续的过程。正如我已经提及的, 这意味着 R/S 尺度的变化比时间的平方根更快;
- 最后, 如果图形呈下降趋势, 我们正在处理一个反持续的过程。
3.3. 分形分析中的记忆概念以及如何界定其深度
为进一步了解分形分析, 我们来介绍一下记忆的概念。
我已经提到过 长线和短线的记忆。在分形分析中, 记忆是一个时间间隔, 在这个时间段期间, 行情会记住过去, 并考虑其对当前和未来事件的影响。该时间间隔是 记忆深度, 其在某种程度上包含分形分析的整体效力和规范。当定义过去的技术形态的相关性时, 这些数据对于技术分析至关重要。
确定记忆深度 不需要过多的处理能力。只需简单地直观分析 V 型统计对数图就足够了。
- 沿所有图形点画一条趋势线。
- 确保曲线不是水平的。
- 定义曲线峰值或函数所能达到的最大值的点。这些最大值作为现有周期的第一个警告。
- 在对数标尺图上定义 X 坐标, 并转换数字, 令其易于理解: 周期长度 = exp^ (对数标尺的周期长度)。因此, 如果您分析了 12000 条 GBPUSD 小时数据, 并在对数标尺图上得到 8.2, 则该周期等于 exp^8.2=3772 小时或 157 天。
- 任何真正的周期应保存在相同的时间帧上, 但以另一个时间帧为基础。例如, 在第 4 页, 我们调查了 12000 条 GBPUSD 小时数据, 并建议存在 157 天的周期。切换到 H4 并分析 12000/4=3000 条数据。如果 157-天周期真实存在, 则您的假定很可能是正确的。如果不是, 那么您可能会找到更短的记忆周期。
3.4. 货币对的实际赫斯特指数值
我们已经介绍完分形分析理论的基本原理。在立即开始利用 MQL5 编程语言实现 RS 分析之前, 我们再来看一些例子。
以下表格显示了不同时间范围内的 11 种外汇货币对的赫斯特指数值, 以及柱线数量。通过使用最小二乘法 (LS) 求解回归来计算比率。正如我们所见, 大多数货币对支持持续的过程, 尽管也有反持续的过程。但是这个结果意义很重大吗?我们可以相信这些数字吗?我们稍后再讨论这个。
表格 1. 分析 2000 根柱线的赫斯特指数
| 品种 | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.559 | 0.513 | 0.567 | 0.577 |
| EURCHF | 0.520 | 0.468 | 0.457 | 0.463 | 0.522 | 0.577 |
| EURJPY | 0.574 | 0.501 | 0.527 | 0.511 | 0.546 | 0.577 |
| EURGBP | 0.553 | 0.571 | 0.540 | 0.562 | 0.550 | 0.577 |
| EURRUB | 柱线不足 | 0.536 | 0.521 | 0.543 | 0.476 | 0.577 |
| USDJPY | 0.591 | 0.563 | 0.583 | 0.519 | 0.565 | 0.577 |
| USDCHF | 柱线不足 | 0.509 | 0.564 | 0.517 | 0.545 | 0.577 |
| USDCAD | 0.549 | 0.569 | 0.540 | 0.519 | 0.565 | 0.577 |
| USDRUB | 0.582 | 0.509 | 0.564 | 0.527 | 0.540 | 0.577 |
| AUDCHF | 0.522 | 0.478c | 0.504 | 0.506 | 0.509 | 0.577 |
| GBPCHF | 0.554 | 0.559 | 0.542 | 0.565 | 0.559 | 0.577 |
表格 2. 分析 400 根柱线的赫斯特指数
| 品种 | H (D1) | H (H4) | H (H1) | H(15M) | H (5M) | E(H) |
|---|---|---|---|---|---|---|
| EURUSD | 0.545 | 0,497 | 0.513 | 0.604 | 0.617 | 0.578 |
| EURCHF | 0.471 | 0.460 | 0.522 | 0.603 | 0.533 | 0.578 |
| EURJPY | 0.545 | 0.494 | 0.562 | 0.556 | 0.570 | 0.578 |
| EURGBP | 0.620 | 0.589 | 0.601 | 0.597 | 0.635 | 0.578 |
| EURRUB | 0.580 | 0.551 | 0.478 | 0.526 | 0.542 | 0.578 |
| USDJPY | 0.601 | 0.610 | 0.568 | 0.583 | 0.593 | 0.578 |
| USDCHF | 0.505 | 0.555 | 0.501 | 0.585 | 0.650 | 0.578 |
| USDCAD | 0.590 | 0.537 | 0.590 | 0.587 | 0.631 | 0.578 |
| USDRUB | 0.563 | 0.483 | 0.465 | 0.531 | 0.502 | 0.578 |
| AUDCHF | 0.443 | 0.472 | 0.505 | 0.530 | 0.539 | 0.578 |
| GBPCHF | 0.568 | 0.582 | 0.616 | 0.615 | 0.636 | 0.578 |
Table 3. M15 和 M5 的赫斯特指数计算结果
| 品种 | H (15M) | 重要性 | H (5M) | 重要性 | E(H) |
|---|---|---|---|---|---|
| EURUSD | 0.543 | 不重要 | 0.542 | 不重要 | 0.544 |
| EURCHF | 0.484 | 重要 | 0.480 | 重要 | 0.544 |
| EURJPY | 0.513 | 不重要 | 0.513 | 不重要 | 0.544 |
| EURGBP | 0.542 | 不重要 | 0.528 | 不重要 | 0.544 |
| EURRUB | 0.469 | 重要 | 0.495 | 重要 | 0.544 |
| USDJPY | 0.550 | 不重要 | 0.525 | 不重要 | 0.544 |
| USDCHF | 0.551 | 不重要 | 0.525 | 不重要 | 0.544 |
| USDCAD | 0.519 | 不重要 | 0.550 | 不重要 | 0.544 |
| USDRUB | 0.436 | 重要 | 0.485 | 重要 | 0.544 |
| AUDCHF | 0.518 | 不重要 | 0.499 | 重要 | 0.544 |
| GBPCHF | 0.533 | 不重要 | 0.520 | 不重要 | 0.544 |
E. Peters 建议分析一些基本时间帧, 并用它来搜索具有周期依赖性的时间序列。之后, 通过改变时间帧及 "拟合" 历史深度, 将所分析的时间间隔切分为较少数量的柱线。这意味着以下内容:
如果在基准时间帧上存在周期, 且如果在不同的分段中发现相同的周期, 则也许可以证明其有效性。
使用可用柱线的不同组合, 我们可以找到非周期循环。它们的长度可以消除以往技术指标信号能用性的任何疑问。
4. 从理论到实践
现在我们已经获得了有关分形分析、赫斯特指数及其数值解析的基本知识, 现在到了利用 MQL5 来实现这个想法的时候了。
我们以下列方式定义技术需求: 我们需要一个程序来计算指定 1000 根历史柱线的赫斯特指数。
步骤 1. 创建一个新脚本
我们得到一个填充了数据的 "存根"。此外, 添加 #property script_show_inputs, 因为我们必须在入口处选择货币对。
//+------------------------------------------------------------------+ //| New.mq5 | //| 版权所有 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| 脚本的 start 函数 | //+------------------------------------------------------------------+ void OnStart() { //--- } //+------------------------------------------------------------------+
步骤 2. 设置收盘价数组, 并检查所选货币对当前是否有 1001 根可用的历史柱线。
为什么在技术需求中设置 1000 根柱线, 而我们却使用 1001 根柱线?答案就是: 需要前一数值的数据来形成对数收益率数组。
double close[]; //声明动态收盘价格数组 int copied=CopyClose(symbol,timeframe,0,barscount1+1,close); //复制所选对的收盘价格至 //close[] 数组 ArrayResize(close,1001); //设置数组大小 ArraySetAsSeries(close,true); if(bars<1001) //为 1001 根历史柱线的存在创造一个条件 { Comment("可用柱线太少了!尝试另一个时间帧。"); Sleep(10000); //标签延迟 10 秒钟 Comment(""); return; }
步骤 3. 创建对数收益率数组。
假定已经声明了 LogReturns 数组, 且存在 ArrayResize(LogReturns, 1001) 语句
for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]);
步骤 4. 计算赫斯特指数。
为能正确分析, 我们需要将分析的历史柱线数量划分为子群, 令每个元素的数量不小于 10。换言之, 我们需要为 1000 找到超过 10 的分频数。有 11 个这样的分频数:
//--- 设置每个子群中的元素数 num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000;
由于我们要计算 RS 统计数据 11 次, 因此开发一个自定义函数是合理的。将要计算的 RS 统计数据子组的最终和初始索引, 以及所要分析的柱线数作为函数参数。算法完全类似于文章开头描述的算法。
//+----------------------------------------------------------------------+ //| R/S 计算函数 | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //初始和为零 DevSum=0.0; //初始累计总和 //偏差为零 //--- 计算收益率总和 for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //累积和 //--- 计算均值 M=Sum/barscount; //--- 计算累计偏差 for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //用于计算偏差的组件 if(DevAccum[i]>MaxValue) //如果数组值小于 MaxValue=DevAccum[i]; //最大值, 分配给 DevAccum 数组元素值 //最大值 if(DevAccum[i]<MinValue) //逻辑是相同的 MinValue=DevAccum[i]; } //--- 计算 R 振幅和 S 偏差 R=MaxValue-MinValue; //幅度是最大值和 MaxValue=0.0; MinValue=1000; //最小值之间的差值 S1=MathSqrt(DevSum/barscount); //计算标准偏差 //--- 计算 R/S 参数 if(S1!=0)RS=R/S1; //消除除零错误 // else Alert("除零!"); return(RS); //返回 RS 统计值 }
使用 switch-case 语句计算。
//--- 计算复合 Log(R/S) for(int A=1; A<=11; A++) //循环允许我们缩短代码 { //此外, 我们考虑所有可能的分频数 switch(A) { case 1: // 100 个群每群包含 10 个元素 { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); //调用 RScuclc 自定义函数 RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: // 50 个群每群包含 20 个元素 { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); //调用 RScuclc 自定义函数 RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; ... ... ... case 9: // 125 和 16 个群 { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: // 125 和 16 个群 { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: //200 和 10 个群 { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } }
步骤 5. 使用最小二乘法 (LS) 法计算线性回归的自定义函数。
输入参数是计算的 RS 统计组件的值。
double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; double N[]; //保存分频对数的数组 double n={10,20,25,40,50,100,125,200,250,500,1000} //频数数组 //---计算 N 比率 for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N1+Y2*N2+Y3*N3+Y4*N4+Y5*N5+Y6*N6+Y7*N7+Y8*N8+Y9*N9+Y10*N10+Y11*N11;
//---计算贝塔回归比率, 或必要的赫斯特指数
b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); }
步骤 6. 用于计算预期 RS 统计值的自定义函数。计算逻辑已在理论部分进行了说明。
//+----------------------------------------------------------------------+ //| 计算预期 E(R/S) 值的函数 | //+----------------------------------------------------------------------+ double ERSculc(double m) //m - 1000 分频数 { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
完整的程序代码也许如下所示:
//+------------------------------------------------------------------+ //| hurst_exponent.mq5 | //| 版权所有 2016, Piskarev D.M. | //| piskarev.dmitry25@gmail.com | //+------------------------------------------------------------------+ #property copyright "版权所有 2016, Piskarev D.M." #property link "piskarev.dmitry25@gmail.com" #property version "1.00" #property script_show_inputs #property strict input string symbol="EURUSD"; // 品种 input ENUM_TIMEFRAMES timeframe=PERIOD_D1; // 时间帧 double LogReturns[],N[], R,S1,DevAccum[],StdDevMas[]; int num1,num2,num3,num4,num5,num6,num7,num8,num9,num10,num11; double pi=3.14159265358979323846264338; double MaxValue=0.0,MinValue=1000.0; double DevSum,Sum,M,RS,RSsum,Dconv; double RS1,RS2,RS3,RS4,RS5,RS6,RS7,RS8,RS9,RS10,RS11, LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8,LogRS9, LogRS10,LogRS11; double rs1[],rs2[],rs3[],rs4[],rs5[],rs6[],rs7[],rs8[],rs9[],rs10[],rs11[]; double E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11; double H,betaE; int bars=Bars(symbol,timeframe); double D,StandDev; //+------------------------------------------------------------------+ //| 脚本的 start 函数 | //+------------------------------------------------------------------+ void OnStart() { double close[]; //声明动态收盘价格数组 int copied=CopyClose(symbol,timeframe,0,1001,close); //复制所选对的收盘价格至 //close[] 数组 ArrayResize(close,1001); //设置数组大小 ArraySetAsSeries(close,true); if(bars<1001) //为 1001 根历史柱线的存在创造一个条件 { Comment("可用柱线太少了!尝试另一个时间帧。"); Sleep(10000); //标签延迟 10 秒钟 Comment(""); return; } //+------------------------------------------------------------------+ //| 准备数组 | //+------------------------------------------------------------------+ ArrayResize(LogReturns,1001); ArrayResize(DevAccum,1001); ArrayResize(StdDevMas,1001); //+------------------------------------------------------------------+ //| 对数收益率数组 | //+------------------------------------------------------------------+ for(int i=1;i<=1000;i++) LogReturns[i]=MathLog(close[i-1]/close[i]); //+------------------------------------------------------------------+ //| | //| R/S 分析 | //| | //+------------------------------------------------------------------+ //--- 设置每个子群中的元素数 num1=10; num2=20; num3=25; num4=40; num5=50; num6=100; num7=125; num8=200; num9=250; num10=500; num11=1000; //--- 计算复合 Log(R/S) for(int A=1; A<=11; A++) { switch(A) { case 1: { ArrayResize(rs1,101); RSsum=0.0; for(int j=1; j<=100; j++) { rs1[j]=RSculc(10*j-9,10*j,10); RSsum=RSsum+rs1[j]; } RS1=RSsum/100; LogRS1=MathLog(RS1); } break; case 2: { ArrayResize(rs2,51); RSsum=0.0; for(int j=1; j<=50; j++) { rs2[j]=RSculc(20*j-19,20*j,20); RSsum=RSsum+rs2[j]; } RS2=RSsum/50; LogRS2=MathLog(RS2); } break; case 3: { ArrayResize(rs3,41); RSsum=0.0; for(int j=1; j<=40; j++) { rs3[j]=RSculc(25*j-24,25*j,25); RSsum=RSsum+rs3[j]; } RS3=RSsum/40; LogRS3=MathLog(RS3); } break; case 4: { ArrayResize(rs4,26); RSsum=0.0; for(int j=1; j<=25; j++) { rs4[j]=RSculc(40*j-39,40*j,40); RSsum=RSsum+rs4[j]; } RS4=RSsum/25; LogRS4=MathLog(RS4); } break; case 5: { ArrayResize(rs5,21); RSsum=0.0; for(int j=1; j<=20; j++) { rs5[j]=RSculc(50*j-49,50*j,50); RSsum=RSsum+rs5[j]; } RS5=RSsum/20; LogRS5=MathLog(RS5); } break; case 6: { ArrayResize(rs6,11); RSsum=0.0; for(int j=1; j<=10; j++) { rs6[j]=RSculc(100*j-99,100*j,100); RSsum=RSsum+rs6[j]; } RS6=RSsum/10; LogRS6=MathLog(RS6); } break; case 7: { ArrayResize(rs7,9); RSsum=0.0; for(int j=1; j<=8; j++) { rs7[j]=RSculc(125*j-124,125*j,125); RSsum=RSsum+rs7[j]; } RS7=RSsum/8; LogRS7=MathLog(RS7); } break; case 8: { ArrayResize(rs8,6); RSsum=0.0; for(int j=1; j<=5; j++) { rs8[j]=RSculc(200*j-199,200*j,200); RSsum=RSsum+rs8[j]; } RS8=RSsum/5; LogRS8=MathLog(RS8); } break; case 9: { ArrayResize(rs9,5); RSsum=0.0; for(int j=1; j<=4; j++) { rs9[j]=RSculc(250*j-249,250*j,250); RSsum=RSsum+rs9[j]; } RS9=RSsum/4; LogRS9=MathLog(RS9); } break; case 10: { ArrayResize(rs10,3); RSsum=0.0; for(int j=1; j<=2; j++) { rs10[j]=RSculc(500*j-499,500*j,500); RSsum=RSsum+rs10[j]; } RS10=RSsum/2; LogRS10=MathLog(RS10); } break; case 11: { RS11=RSculc(1,1000,1000); LogRS11=MathLog(RS11); } break; } } //+----------------------------------------------------------------------+ //| 计算赫斯特指数 | //+----------------------------------------------------------------------+ H=RegCulc1000(LogRS1,LogRS2,LogRS3,LogRS4,LogRS5,LogRS6,LogRS7,LogRS8, LogRS9,LogRS10,LogRS11); //+----------------------------------------------------------------------+ //| 计算预期 log(E(R/S)) 值 | //+----------------------------------------------------------------------+ E1=MathLog(ERSculc(num1)); E2=MathLog(ERSculc(num2)); E3=MathLog(ERSculc(num3)); E4=MathLog(ERSculc(num4)); E5=MathLog(ERSculc(num5)); E6=MathLog(ERSculc(num6)); E7=MathLog(ERSculc(num7)); E8=MathLog(ERSculc(num8)); E9=MathLog(ERSculc(num9)); E10=MathLog(ERSculc(num10)); E11=MathLog(ERSculc(num11)); //+----------------------------------------------------------------------+ //| 计算预期的贝塔 E(R/S) 值 | //+----------------------------------------------------------------------+ betaE=RegCulc1000(E1,E2,E3,E4,E5,E6,E7,E8,E9,E10,E11); Alert("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); Comment("H= ", DoubleToString(H,3), " , E= ",DoubleToString(betaE,3)); } //+----------------------------------------------------------------------+ //| R/S 计算函数 | //+----------------------------------------------------------------------+ double RSculc(int bottom,int top,int barscount) { Sum=0.0; //初始和为零 DevSum=0.0; //初始累计总和 //偏差为零 //--- 计算收益率总和 for(int i=bottom; i<=top; i++) Sum=Sum+LogReturns[i]; //累积和 //--- 计算均值 M=Sum/barscount; //--- 计算累计偏差 for(int i=bottom; i<=top; i++) { DevAccum[i]=LogReturns[i]-M+DevAccum[i-1]; StdDevMas[i]=MathPow((LogReturns[i]-M),2); DevSum=DevSum+StdDevMas[i]; //用于计算偏差的组件 if(DevAccum[i]>MaxValue) //如果数组值小于 MaxValue=DevAccum[i]; //最大值, 分配给 DevAccum 数组元素值 //最大值 if(DevAccum[i]<MinValue) //逻辑是相同的 MinValue=DevAccum[i]; } //--- 计算 R 振幅和 S 偏差 R=MaxValue-MinValue; //幅度是最大值和 MaxValue=0.0; MinValue=1000; //最小值之间的差值 S1=MathSqrt(DevSum/barscount); //计算标准偏差 //--- 计算 R/S 参数 if(S1!=0)RS=R/S1; //消除除零错误 // else Alert("除零!"); return(RS); //返回 RS 统计值 } //+----------------------------------------------------------------------+ //| 回归计算器 | //+----------------------------------------------------------------------+ double RegCulc1000(double Y1,double Y2,double Y3,double Y4,double Y5,double Y6, double Y7,double Y8,double Y9,double Y10,double Y11) { double SumY=0.0; double SumX=0.0; double SumYX=0.0; double SumXX=0.0; double b=0.0; //保存分频对数的数组 double n[]={10,20,25,40,50,100,125,200,250,500,1000}; //分频数数组 //---计算 N 比率 ArrayResize(N,11); for (int i=0; i<=10; i++) { N[i]=MathLog(n[i]); SumX=SumX+N[i]; SumXX=SumXX+N[i]*N[i]; } SumY=Y1+Y2+Y3+Y4+Y5+Y6+Y7+Y8+Y9+Y10+Y11; SumYX=Y1*N[0]+Y2*N[1]+Y3*N[2]+Y4*N[3]+Y5*N[4]+Y6*N[5]+Y7*N[6]+Y8*N[7]+Y9*N[8]+Y10*N[9]+Y11*N[10]; //---计算贝塔回归比率, 或必要的赫斯特指数 b=(11*SumYX-SumY*SumX)/(11*SumXX-SumX*SumX); return(b); } //+----------------------------------------------------------------------+ //| 计算预期 E(R/S) 值的函数 | //+----------------------------------------------------------------------+ double ERSculc(double m) //m - 1000 分频数 { double e; double nSum=0.0; double part=0.0; for(int i=1; i<=m-1; i++) { part=MathPow(((m-i)/i), 0.5); nSum=nSum+part; } e=MathPow((m*pi/2),-0.5)*nSum; return(e); }
您可以自行实现更广泛的计算功能并创建一个用户友好的图形界面来升级代码。
在最后一个章节中, 我们将讨论现有的软件解决方案。
5. 软件解决方案
有多个软件资源实现了 R/S 分析算法。然而, 算法实现通常是压缩的, 大部分的分析工作留给了用户。其中一个资源是 Matlab 软件包。
在 市场 中还有一个名为 分形分析 的 MetaTrader 5 实用程序, 允许用户对金融市场进行分形分析。我们来近距离看看吧。
5.1. 输入
事实上, 我们只需要整个变量中的前三个输入参数 (品种, 柱线数和时间帧)。
正如我们在下面的屏幕截图中所见, 分形分析允许选择一个货币对, 无论实用程序的品种窗口是否启动: 最重要的是在初始化窗口中指定一个品种。
选择参数中的某个指定时间帧的柱线数量。
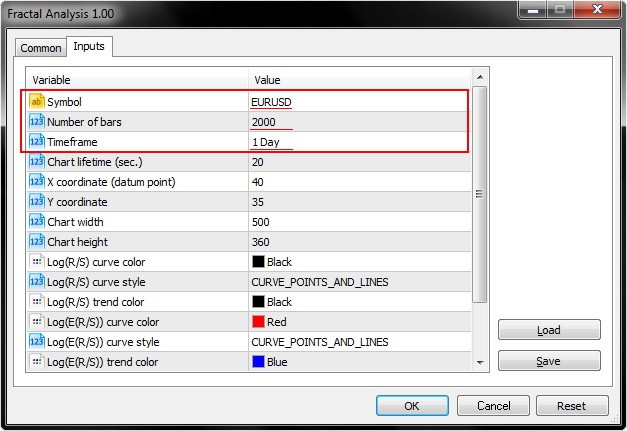
还有, 请注意为图表生命周期参数设置秒数, 您可以在其中使用实用程序。点击确定之后, 分析器将显示在 MetaTrader 5 主终端窗口的左上角。该示例显示在下面的屏幕截图上。
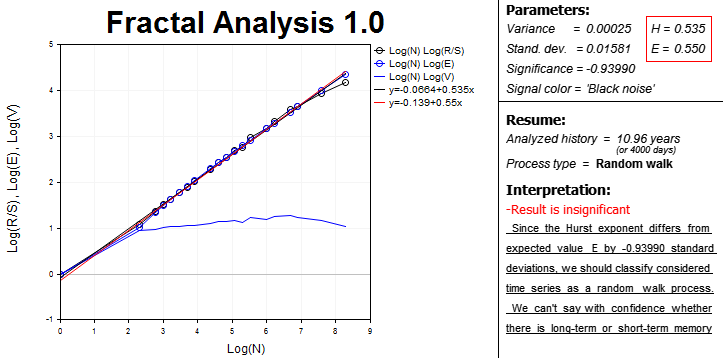
最终, 分形分析所需的所有数据和结果出现在屏幕上, 且合并成块。
左侧部分带图形区域依赖对数标尺:
- R/S 统计来自样本中一定数量的观测值;
- 观测次数的预期 R/S 统计值 E(R/S);
- 观测次数的 V 形统计。
这是一个涉及 MetaTrader 5 所用的图表分析工具的交互区域, 因为有时很难在没有特殊手段的情况下定义周期长度。
还存在曲线和趋势线方程。趋势线的斜率用于定义数值化赫斯特指数 (H)。预期赫斯特指数 (E) 也一并计算。这些方程在右边相邻的区块。在此还计算发散, 分析意义以及信号光谱颜色。
出于便利, 本程序以日为单位计算分析周期的长度。在评估历史数据的意义时要牢记这一点。
"Process type" 一行指定时间序列参数:
- 持久性;
- 反持久性;
- 随机游走。
最后, 解释模块显示一个简短的摘要, 可以对分形分析领域的新手有所帮助。
5.2. 操作实例
我们应定义将要用于分析的品种和时间帧。我们取 NZDCHF, 看看H1 周期最后一笔报价。
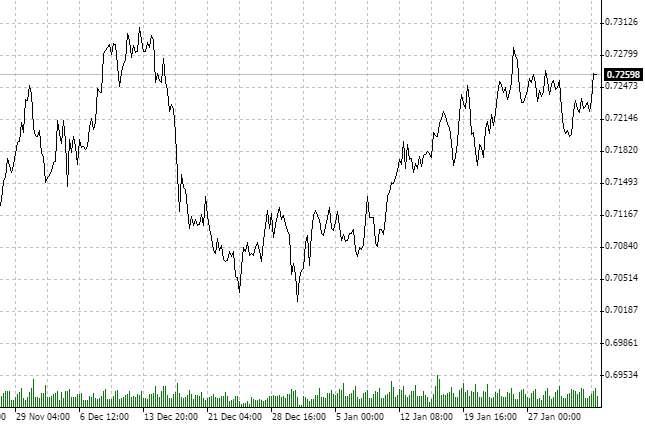
请注意, 大约在过去两个月里行情一直在巩固。再次强调, 我们对其它投资边际不感兴趣。很有可能在 D1 图表显示出上涨或下跌。我们已选择 H1 以及一定数量的历史数据。
显而易见, 这个过程是反持续性的。让我们用分形分析来检查它。
从 11 月 21 日到 2 月 3 日, 我们有 75 日的历史。将 75 天转换至小时后, 我们会收到 1800 个小时的数据。由于实用程序进入时还没有很多柱线, 指定最近的值 — 2000 个分析过的小时周期。
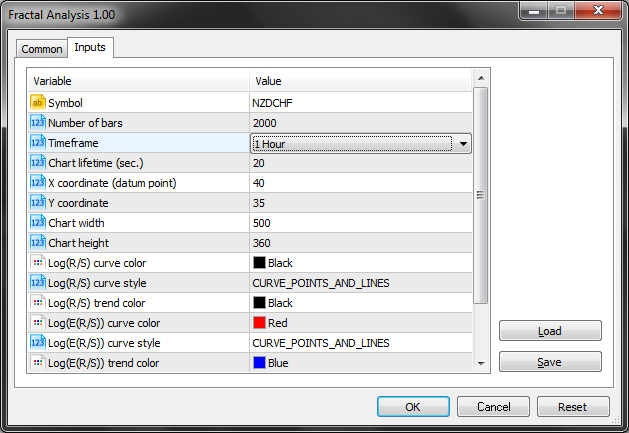
结果显示如下:
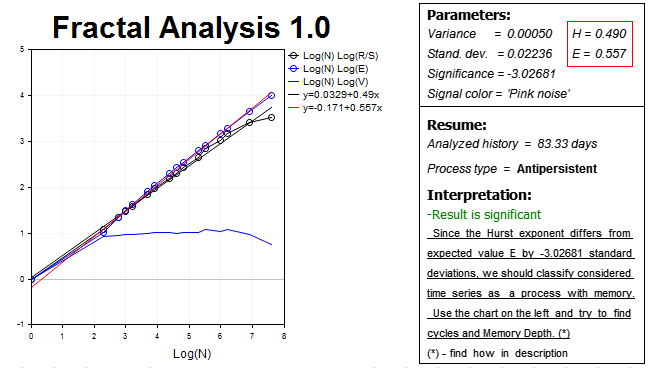
因此, 我们的假设得到了证实, 行情在此边际内展示了反持续性过程 — 赫斯特指数 H=0.490, 几乎比预期值 E=0.557 低了三个标准偏差。
我们来修正结果, 并使用一个 略高一点的时间帧 (H2), 相应地历史记录中的柱线数量少了两倍 (1000 个值)。结果如下:
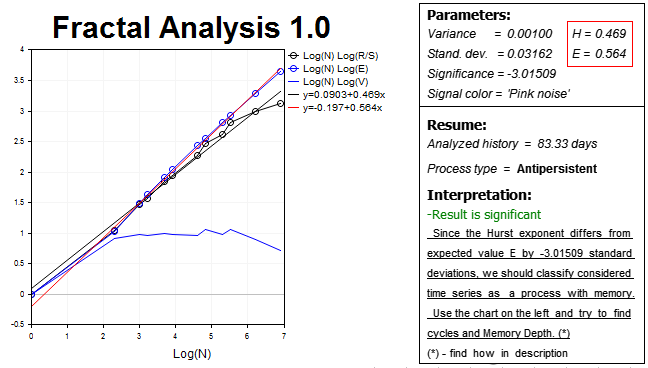
我们再次看到反持续的过程。赫斯特指数 H=0.469 比预期指数值 E=0.564 低于三个以上的标准偏差。
现在, 我们来尝试 发现周期。
我们应该返回到 H1 图表, 并定义 R/S 曲线与 E(R/S) 分叉的时刻。这一刻的特征是在 V 型统计图上形成了一个顶点。因此, 我们能够定义近似的周期大小。
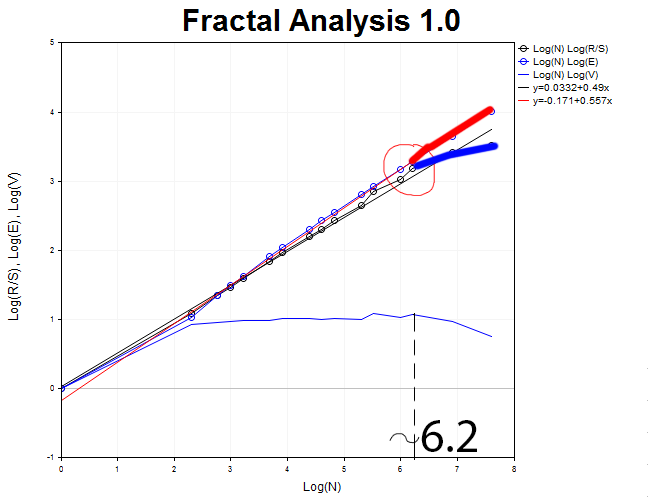
大约等于 N1 = 2.71828^6.2 = 493 H1, 相当于 21 日。
当然, 单个实验并不能保证其结果的可靠性。如上所述, 有必要尝试不同的时间帧, 并选择各种 "时间帧 — 柱线数" 组合, 以便确保结果有效。
我们来针对 H2 时间帧内的 1000 根柱线进行一遍图形分析。
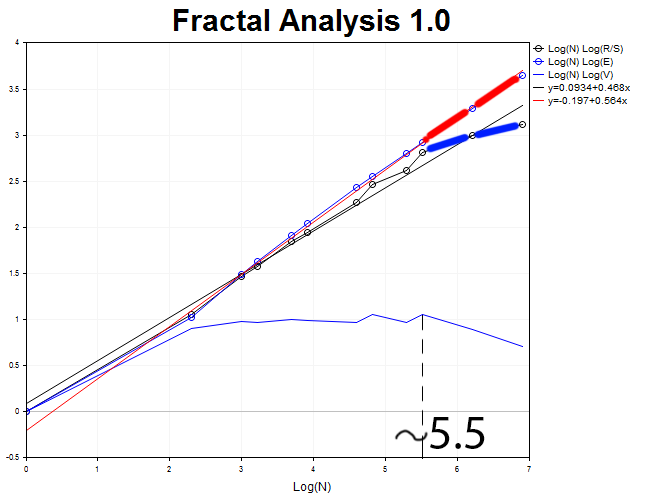
周期长度等于 N2 = 2.71828^5.5 = 245 H2 (约二十日)。
现在, 我们来分析 M30 时间帧和 4000 个值。我们获得赫斯特指数 H = 0.492 的反持续过程, 且预期值 E=0.55 超过 H 值达 3.6 个标准偏差。
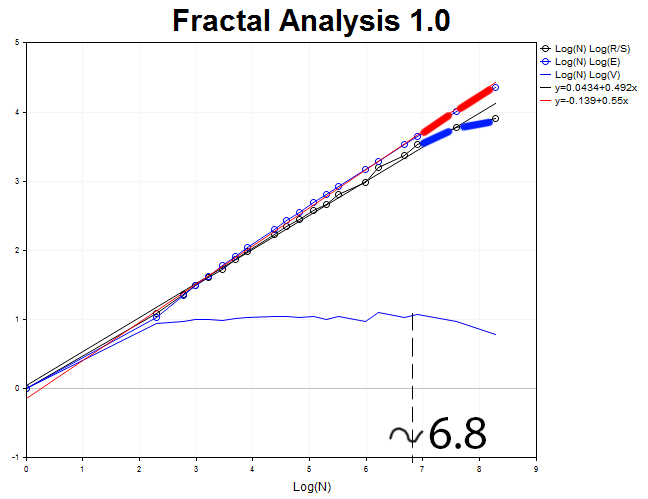
周期长度 N3 = 2.71828^6.8 = 898 M30 (18.7 日)。
三个测试对于训练示例足够了。我们来寻找所获周期长度的均值 M= (N1 + N2 + N3)/3 = (21 + 20 + 18.7)/3 = 19.9 (20 日)。
结果就是, 我们获得了技术数据足够可靠的周期, 可用于制订交易策略。正如我已经提及的, 上面提供的计算和分析是为期两个月的投资边际。这意味着该分析与日内交易无关, 因为它可能具有自己的超短线周期过程, 我们必须证明其存在或不存在。如果没有检测到这些周期, 技术分析将失去其相关性和效率。在此情况下, 消息交易并定义市场情绪是最合理的解决方案。
结论
分形分析是技术分析, 基本面和统计方法的一种有效协同手段, 用来预测行情的动态。这是一种多能的数据处理方法: R/S 分析和赫斯特指数在地理、生物学、物理和经济学领域均已得到成功应用。分形分析可用于开发银行应用的评分或评估模型, 分析借款人的偿付能力。
正如我在文章开头已经说过的: 为了外汇交易成功, 我们需要比其他投资者了解更多一些。预料在此会有一些误会, 我想提醒读者, 市场往往会 "欺骗" 分析师。因此, 请务必始终检查更高和更低时间帧内是否存在非周期性循环。如果在其它时间帧里没有检测到, 则此周期很有可能只是一个市场噪音。


