内容

• 概述
1. 准备初始数据
2. 处理 pretrain 子集中的噪声样本
3. 针对去噪初始数据训练神经网络分类器的融合，并基于测试子集计算神经网络的连续预测
4. 确定所获的连续预测的阈值，将它们转换为类标签，并计算神经网络的度量
5. 测试融合
6. 优化神经网络分类器融合的超参数
7. 优化后期处理超参数
8. 将若干最佳融合组合成一个超级融合，还有它们的输出
9. 分析实验结果
• 结束语
• 附件

概述

在前两篇文章（1，2）中，我们创建了一组 ELM 神经网络分类器。 那时我们讨论了如何改进分类品质。 在许多可能的解决方案中，选择了两个：减少噪声样本的影响并选择最佳阈值，通过该阈值，将融合的神经网络的连续预测转换为类标签。 在本文中，我建议通过实验来测试分类品质如何受以下因素影响： 

• 数据降噪方法,
  
• 阈值类型,
  
• 融合神经网络的超参数优化和后期处理。
  

之后比较两种方法的分类品质：通过平均获得的分类品质，以及由多个优化结果组成的超级融合的简单多数表决分类品质。 所有计算都在 R 3.4.4 环境中执行。

1. 准备初始数据

为了准备初始数据，我们将使用以前描述过的 脚本。

在 第一个 模块（Library）中，加载必要的函数和函数库。

在 第二个 模块 (prepare) 中, 使用终端传递过来的含时间戳的报价，计算指标值（在这种情况下，这些是数字滤波器）和基于 OHLC 的其它变量。 将此数据集合并到数据帧 dt 中。 然后在这些数据中定义异常值的参数并对其进行估算。 然后定义规范化参数并规范化数据。 我们得到了一组输入数据 DTcap.n。

在 第三个 模块 (Data X1) 中, 生成两个集合:

• data1 — 包含带有 Data 时间戳和 Class 目标的全部 13 个指标;
• X1 — 同一组预测变量，但没有时间戳。 目标将转换为数值（0,1）。

在 第四个 模块 (Data X2) 中, 也生成两个集合:

• data2 — 包含 7 个预测变量和一个时间戳 (Data, CO, HO, LO, HL, dC, dH, dL);
• Х2 — 相同的预测因子，但没有时间戳。

路径 patch 指向的脚本文件位置由用户定义。

#--1--Library-------------
patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/"
source(file = paste0(patch,"importar.R"))
source(file = paste0(patch,"Library.R"))
source(file = paste0(patch,"FunPrepareData_VII.R"))
source(file = paste0(patch,"FUN_Stacking_VIII.R"))
import_fun(NoiseFiltersR, GE, noise)
#--2-prepare----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign",
  preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95))
  DTcap.n <- NormData(DTcap, preproc = preproc)
}, env)

#--3-Data X1-------------
evalq({
  subset <- qc(pretrain, train, test, test1)
  foreach(i = 1:length(DTcap.n)) %do% {
    DTcap.n[[i]] ->.;  
    dp$select(., Data, ftlm, stlm, rbci, pcci, fars, 
              v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, 
              v.stlm, v.rbci, v.pcci, Class)} -> data1
  names(data1) <- subset
  X1 <- vector(mode = "list", 4)
  foreach(i = 1:length(X1)) %do% {
    data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x
    data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y
    list(x = x, y = y)} -> X1
  names(X1) <- subset
}, env)
#--4-Data-X2-------------
evalq({
  foreach(i = 1:length(DTcap.n)) %do% {
    DTcap.n[[i]] ->.;  
    dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2
  names(data2) <- subset
  X2 <- vector(mode = "list", 4)
  foreach(i = 1:length(X2)) %do% {
    data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x
    DT[[i]]$dz -> y
    list(x = x, y = y)} -> X2
  names(X2) <- subset
  rm(dt, DT, pre.outl, DTcap, meth, preproc)
}, env)

在 第五个 模块 (bestF) 中, 按重要性 (orderX1) 的升序对 Х1 预测值进行排序。 选择系数高于0.5（featureX1）的那些。 输出所选预测因子的系数和名称。

#--5--bestF-----------------------------------
#require(clusterSim)
evalq({
  orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
         distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
         #"d3" - Chebychev (max), "d4" - squared Euclidean, 
         #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
         method = "kmeans" ,#"kmeans" (default) , "single", 
         #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
         #"median", "centroid", "pam"
         Index = "cRAND") -> rx1
  rx1$stopri[ ,1] -> orderX1
  featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% 
    dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1$stopri)
      [,1]      [,2]
 [1,]    6 1.0423206
 [2,]   12 1.0229287
 [3,]    7 0.9614459
 [4,]   10 0.9526798
 [5,]    5 0.8884596
 [6,]    1 0.8055126
 [7,]    3 0.7959655
 [8,]   11 0.7594309
 [9,]    8 0.6960105
[10,]    2 0.6626440
[11,]    4 0.4905196
[12,]    9 0.3554887
[13,]   13 0.2269289
colnames(env$X1$pretrain$x)[env$featureX1]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars"   "ftlm"   "rbci"   "v.stlm" "v.rftl"
[10] "stlm"

对第二数据集合 Х2 进行相同的计算。 我们获得 orderX2 和 featureX2。

evalq({
  orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
         distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
         #"d3" - Chebychev (max), "d4" - squared Euclidean, 
         #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
         method = "kmeans" ,#"kmeans" (default) , "single", 
         #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
         #"median", "centroid", "pam"
         Index = "cRAND") -> rx2 
  rx2$stopri[ ,1] -> orderX2
  featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>% 
    dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
     [,1]      [,2]
[1,]    1 1.6650259
[2,]    5 1.6636689
[3,]    3 0.7751799
[4,]    2 0.7751351
[5,]    6 0.5692846
[6,]    7 0.5496889
[7,]    4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"

这样就完成了实验初始数据的准备。 我们已经准备好按重要性排序的两个数据集 X1/data1，X2/data2 和预测因子 orderX1，orderX2。 以上所有脚本都位于 Prepare_VIII.R 文件中。

2. 处理 pretrain 子集中的噪声样本

许多文章的作者，包括我自己，都为过滤噪声预测因子出版刊物。 在此，我建议探索另一个同样重要但功能较少的特性 — 识别并处理数据集合当中的噪声样本。 那么为什么数据集合中的一些样本会被认为是噪声，哪些方法可以用来处理它们呢？ 我会尝试解释。

因此，我们面临着分类的任务，同时我们有一套预测因子训练集合和目标。 该目标被认为与训练集合的内部结构很好地对应。 但实际上，预测因子集合的数据结构比目标的拟议结构复杂得多。 事实证明，该集合包含与目标相对应的样本，而有些则完全不对应，在训练时会极大地令模型扭曲。 结果就是，导致模型分类的品质降低。 识别和处理噪声样本的方法已有详尽 研讨。 在此，我们检查分类品质如何受三种处理方法的影响:

• 错误纠正标记的样本;
• 将它们从集合中移除;
• 将它们分配给一个单独的类。

使用 NoiseFiltersR::GE() 函数识别和处理噪声样本。 它查找噪声样本并修改其标签（纠正错误标签）。 不能重新标记的样本将被删除。 识别出的噪声样本也可以手动从集合中删除，或者移至单独的类中，为它们分配新的标签。 上面的所有计算都在 'pretrain' 子集上执行，因为它将用于训练融合。 查看函数的结果:

#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
  out <- noise(x = data1[[1]] %>% dp$select(-Data))
  summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset 

Call:
GE(x = data1[[1]] %>% dp$select(-Data))

Parameters:
k: 5
kk: 3

Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)

Explicit indexes for removed instances:
.......

out 函数的输出结构:

> str(env$out)
List of 7
 $ cleanData :'data.frame':     4001 obs. of  14 variables:
  ..$ ftlm  : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ...
  ..$ stlm  : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ...
  ..$ rbci  : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ...
  ..$ pcci  : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ...
  ..$ fars  : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ...
  ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ...
  ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ...
  ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ...
  ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ...
  ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ...
  ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ...
  ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ...
  ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ...
  ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
 $ remIdx    : int(0) 
 $ repIdx    : int [1:819] 16 27 30 31 32 34 36 38 46 58 ...
 $ repLab    : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ...
 $ parameters:List of 2
  ..$ k : num 5
  ..$ kk: num 3
 $ call      : language GE(x = data1[[1]] %>% dp$select(-Data))
 $ extraInf  : NULL
 - attr(*, "class")= chr "filter"

其中:

• out$cleanData — 噪声样本标记经纠正后的数据集合， 
• out$remIdx — 已删除样本的索引（样本中没有）, 
• out$repIdx — 重新标记目标的样本索引,
• out$repLab — 这些噪音样本的新标签。 因此，我们可以使用 out$repIdx 从集合中删除它们或为它们分配新标签。

一旦确定了噪声样本的索引，就可以准备用于训练融合的四个数据集合，合并到 denoiseX1pretrain 结构中。

• denoiseX1pretrain$origin — 原始 pretraining 集合;
• denoiseX1pretrain$repaired — 已矫正噪声样本的标签数据集合;
• denoiseX1pretrain$removed — 已删除噪声样本的数据集合;
• denoiseX1pretrain$relabeled — 分配新标签噪声样本的数据集合（即，目标现在有三个类）。

#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
  out <- noise(x = data1$pretrain %>% dp$select(-Data))
  Yrelab <- X1$pretrain$y
  Yrelab[out$repIdx] <- 2L
  X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data) 
  denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x,  y = X1$pretrain$y),
                            repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>% 
                                             as.numeric() %>% subtract(1)), 
                             removed = list(x = X1rem %>% dp$select(-Class), 
                                          y = X1rem$Class %>% as.numeric() %>% subtract(1)),
                             relabeled = list(x = X1$pretrain$x, y = Yrelab))
  rm(out, Yrelab, X1rem)     
}, env)

子集 denoiseX1pretrain$origin|modified|relabeled 具有相同的预测因子 х，但目标 y 在每个集合中都不同。 我们来看看它们的结构:

#-------------------------
env$denoiseX1pretrain$repaired$x  %>% str()
'data.frame':   4001 obs. of  13 variables:
 $ ftlm  : num  0.293 0.492 0.47 0.518 0.395 ...
 $ stlm  : num  0.204 0.185 0.161 0.153 0.142 ...
 $ rbci  : num  -0.0434 0.1156 0.1501 0.25 0.248 ...
 $ pcci  : num  -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ...
 $ fars  : num  0.208 0.255 0.246 0.279 0.267 ...
 $ v.fatl: num  0.4963 0.4635 0.0842 0.3707 0.0542 ...
 $ v.satl: num  -0.0146 0.0248 -0.0353 0.1797 0.1205 ...
 $ v.rftl: num  -0.2695 -0.0809 0.1752 0.3637 0.5305 ...
 $ v.rstl: num  0.398 0.362 0.386 0.374 0.357 ...
 $ v.ftlm: num  0.5244 0.4039 -0.0296 0.1088 -0.2299 ...
 $ v.stlm: num  -0.275 -0.226 -0.285 -0.11 -0.148 ...
 $ v.rbci: num  0.5374 0.4811 0.0978 0.2992 -0.0141 ...
 $ v.pcci: num  -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ...
env$denoiseX1pretrain$relabeled$x  %>% str()
'data.frame':   4001 obs. of  13 variables:
 $ ftlm  : num  0.293 0.492 0.47 0.518 0.395 ...
 $ stlm  : num  0.204 0.185 0.161 0.153 0.142 ...
 $ rbci  : num  -0.0434 0.1156 0.1501 0.25 0.248 ...
 $ pcci  : num  -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ...
 $ fars  : num  0.208 0.255 0.246 0.279 0.267 ...
 $ v.fatl: num  0.4963 0.4635 0.0842 0.3707 0.0542 ...
 $ v.satl: num  -0.0146 0.0248 -0.0353 0.1797 0.1205 ...
 $ v.rftl: num  -0.2695 -0.0809 0.1752 0.3637 0.5305 ...
 $ v.rstl: num  0.398 0.362 0.386 0.374 0.357 ...
 $ v.ftlm: num  0.5244 0.4039 -0.0296 0.1088 -0.2299 ...
 $ v.stlm: num  -0.275 -0.226 -0.285 -0.11 -0.148 ...
 $ v.rbci: num  0.5374 0.4811 0.0978 0.2992 -0.0141 ...
 $ v.pcci: num  -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ...
env$denoiseX1pretrain$repaired$y  %>% table()
.
   0    1 
1888 2113 
env$denoiseX1pretrain$removed$y  %>% table()
.
   0    1 
1509 1673
env$denoiseX1pretrain$relabeled$y  %>% table()
.
   0    1    2 
1509 1673  819 

由于集合 denoiseX1pretrain$removed 中的样本数量已变化，我们来检查预测因子的重要性如何变化:

evalq({
  orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(), 
         type = "metric", s = 1, 4, 
         distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
         #"d3" - Chebychev (max), "d4" - squared Euclidean, 
         #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
         method = "kmeans" ,#"kmeans" (default) , "single", 
         #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
         #"median", "centroid", "pam"
         Index = "cRAND") -> rx1rem
  rx1rem$stopri[ ,1] -> orderX1rem
  featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(), 
                            rx1rem$stopri[ ,2] > 0.5) %>% 
    dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
     [,1]      [,2]
 [1,]    6 1.0790642
 [2,]   12 1.0320772
 [3,]    7 0.9629750
 [4,]   10 0.9515987
 [5,]    5 0.8426669
 [6,]    1 0.8138830
 [7,]    3 0.7934568
 [8,]   11 0.7682185
 [9,]    8 0.6720211
[10,]    2 0.6355753
[11,]    4 0.5159589
[12,]    9 0.3670544
[13,]   13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars"   "ftlm"   "rbci"   "v.stlm" "v.rftl"
[10] "stlm"   "pcci" 

最佳预测因子的顺序和组成发生了变化。 在训练融合时需要考虑到这一点。

因此，我们准备了 4 个子集：denoiseX1pretrain$origin，修复，删除，重新标记。 它们将用于训练 ELM 融合。 数据去噪脚本位于 Denoise.R文件中。 初始数据 Х1 和 denoiseX1pretrain 的结构如下所示:

图例 1. 初始数据的结构。

3. 针对去噪初始数据训练神经网络分类器的融合，并基于测试子集计算神经网络的连续预测

我们编写一个函数来训练融合并接收预测因子，稍后它们将作为堆叠融合中可训练组合器的输入数据。

此类计算已在 上一篇文章 中执行，因此，不会讨论它们的详细信息。 简而言之:

• 在模块1（输入）中，定义常量;
  
• 在模块 2（createEns）中，定义函数 CreateEns()，它将创建含有常量参数和可再现初始化的单独神经网络分类器的融合;
  
• 在模块 3（GetInputData）中，GetInputData() 函数使用融合 Ens 计算三个子集 Х1$train/test/test1 的预测因子。

  通过随机数发生器（RNG）的常量和相同的初始化来提供再现性。 脚本位于 FUN_Stacking_VIII.R 文件里

#--1--Input-------------
evalq({
  #type of activation function. 
  Fact <- c("sig", #: sigmoid
            "sin", #: sine
            "radbas", #: radial basis
            "hardlim", #: hard-limit
            "hardlims", #: symmetric hard-limit
            "satlins", #: satlins
            "tansig", #: tan-sigmoid
            "tribas", #: triangular basis
            "poslin", #: positive linear
            "purelin") #: linear
  n <- 500
  r = 7L
  SEED <- 12345
  #--2-createENS----------------------
  createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){
    Xtrain <- X[ , featureX1] 
    k <- 1
    rng <- RNGseq(n, SEED)
    #---creste Ensemble---
    Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr
      k <- k + 1
      elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact])
    }
    return(Ens)
  }
  #--3-GetInputData -FUN-----------
  GetInputData <- function(Ens, X, Y){
    #---predict-InputPretrain--------------
    Xtrain <- X[ ,featureX1]
    k <- 1
    rng <- RNGseq(n, SEED)
    #---create Ensemble---
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr
      k <- k + 1
      predict(Ens[[i]], newdata = Xtrain[-idx, ])
    } %>% unname() -> InputPretrain
    #---predict-InputTrain--
    Xtest <- X1$train$x[ , featureX1]
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest)
    } -> InputTrain #[ ,n]
    #---predict--InputTest----
    Xtest1 <- X1$test$x[ , featureX1]
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest1)
    } -> InputTest #[ ,n]
    #---predict--InputTest1----
    Xtest2 <- X1$test1$x[ , featureX1]
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest2)
    } -> InputTest1 #[ ,n]
    #---res-------------------------
    return(list(InputPretrain = InputPretrain,
                InputTrain = InputTrain,
                InputTest = InputTest,
                InputTest1 = InputTest1))
  }
}, env) 

我们已有的 denoiseX1pretrain 集合含四组用于训练融合的数据：原始（origin），含校正标签（repaired），含移除（removed）和重新标记（relabeled）的噪声样本。 针对这些数据组中的每一组进行融合训练之后，我们获得了四个融合。 将这些融合与 GetInputData() 函数一起使用，我们在三个子集中获得四组预测因子： train，test 和 test1。 下面的脚本分别用于每个扩展形式的融合（仅用于调试和易于理解）。

#---4--createEns--origin--------------
evalq({
  Ens.origin <- vector(mode = "list", n)
  res.origin <- vector("list", 4)
  x <- denoiseX1pretrain$origin$x %>% as.matrix()
  y <- denoiseX1pretrain$origin$y
  createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin
  GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin
}, env)
#---4--createEns--repaired--------------
evalq({
  Ens.repaired <- vector(mode = "list", n)
  res.repaired <- vector("list", 4)
  x <- denoiseX1pretrain$repaired$x %>% as.matrix()
  y <- denoiseX1pretrain$repaired$y
  createEns(r = 7L, nh = 5L, fact = 7L,  X = x, Y = y) -> Ens.repaired
  GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired
}, env)
#---4--createEns--removed--------------
evalq({
  Ens.removed <- vector(mode = "list", n)
  res.removed <- vector("list", 4)
  x <- denoiseX1pretrain$removed$x %>% as.matrix()
  y <- denoiseX1pretrain$removed$y
  createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed
  GetInputData(Ens = Ens.removed,  X = x, Y = y) -> res.removed
}, env)
#---4--createEns--relabeled--------------
evalq({
  Ens.relab <- vector(mode = "list", n)
  res.relab <- vector("list", 4)
  x <- denoiseX1pretrain$relabeled$x %>% as.matrix()
  y <- denoiseX1pretrain$relabeled$y
  createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab
  GetInputData(Ens = Ens.relab,  X = x, Y = y) -> res.relab
}, env)

融合预测结果的结构如下所示:

> env$res.origin %>% str()
List of 4
 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ...
 $ InputTrain   : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ...
 $ InputTest    : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ...
 $ InputTest1   : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ...
> env$res.repaired %>% str()
List of 4
 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ...
 $ InputTrain   : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ...
 $ InputTest    : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ...
 $ InputTest1   : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ...
> env$res.removed %>% str()
List of 4
 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ...
 $ InputTrain   : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ...
 $ InputTest    : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ...
 $ InputTest1   : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ...
> env$res.relab %>% str()
List of 4
 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ...
 $ InputTrain   : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ...
 $ InputTest    : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ...
 $ InputTest1   : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...

我们来看看这些输出/输入的分布情况如何。 查看 InputTrain[, 1:10] 集合的前 10 个输出:

#------Ris InputTrain------
par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2))
boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
par(mfrow = c(1, 1))

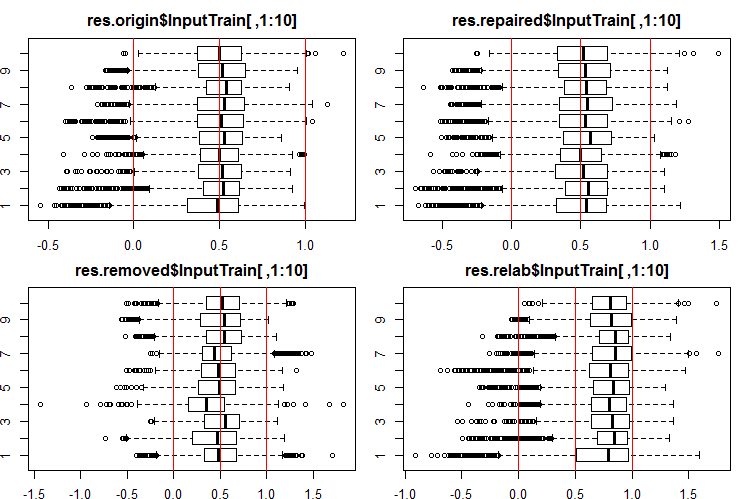
图例 2. 使用四个不同的融合，InputTrain 的输出预测分布。

查看 InputTest[ ,1:10] 集合的前 10 个输出:

#------Ris InputTest------
par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1)

boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
par(mfrow = c(1, 1))

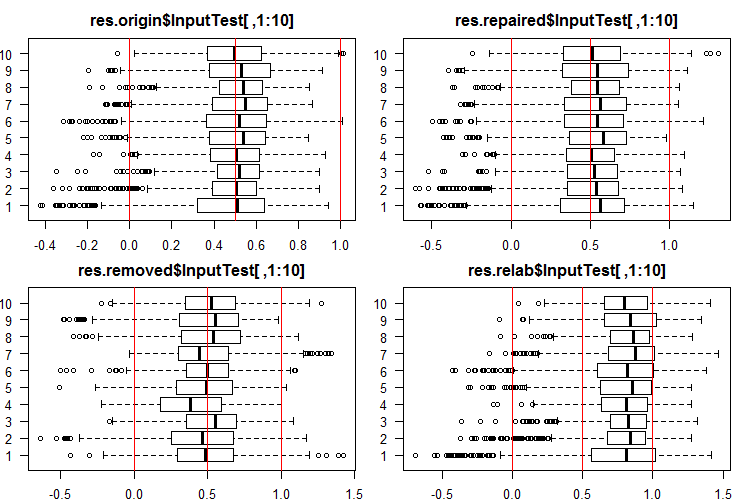
图例 3. 使用四个不同的融合，InputTest 的输出预测分布。

查看 InputTest1[ ,1:10] 集合的前 10 个输出:

#------Ris InputTest1------
par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2))
boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]")
abline(v = c(0, 0.5, 1.0), col = 2)
par(mfrow = c(1, 1))

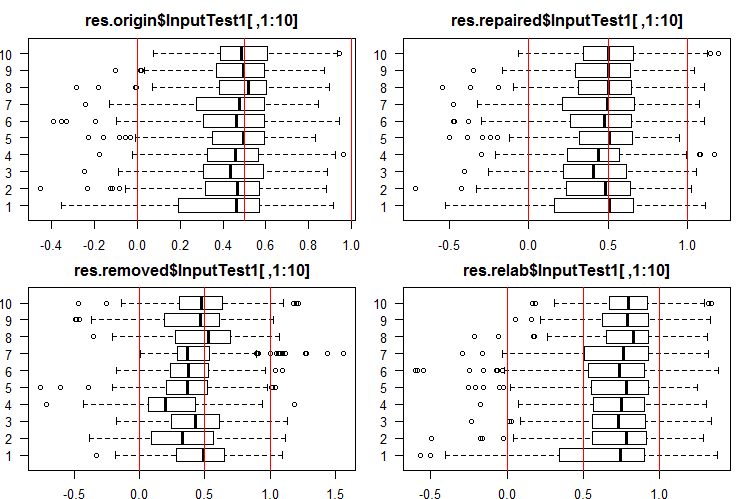
图例 4. 使用四个不同的融合，InputTest1 的输出预测分布。

所有预测的分布与通过先前实验中 SpatialSign 方法常规化的数据获得的预测大不相同。 您可以自行尝试不同的规范化方法。

在使用每个融合计算子集 X1$train/test/test1 的预测之后，我们获得四组数据 — res.origin，res.repaired，res.removed 和 res.relab，分布如图例 2 — 4 所示。 

我们来判断每个融合的分类品质，将连续预测转换为类标签。 

4. 确定所获的连续预测的阈值，将它们转换为类标签，并计算神经网络的度量

为了将连续数据转换为类标签，需用到一个或多个阈值来划分这些类。 从所有融合的第五个神经网络所获 InputTrain 集合的连续预测如下:

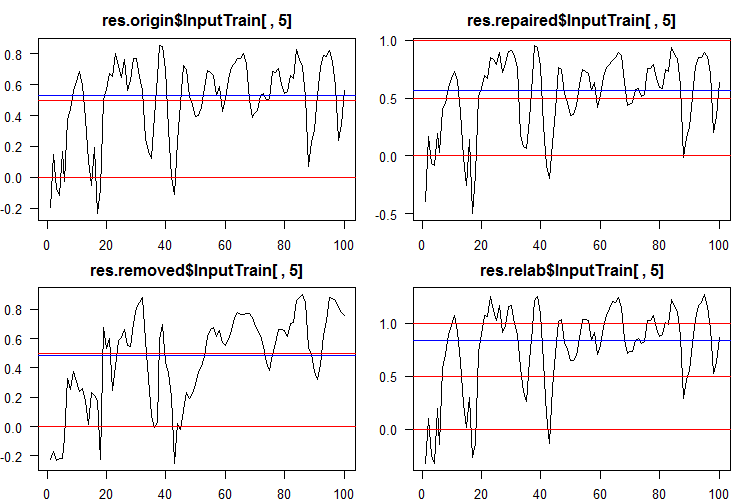
图例 5. 各种融合的第五神经网络的连续预测。

如您所见，origin, repaired, relabeled 模型的连续预测图形在形状上相似，但具有不同的范围。 removed 模型的预测线在形状上有很大差异。

为简化后续计算，请在一个结构 predX1 中收集所有模型及其预测。 为此，编写一个紧凑的函数，它将在循环中重复所有的计算。 此为脚本和 predX1 结构图片:

library("doFuture")
#---predX1------------------
evalq({
  group <- qc(origin, repaired, removed, relabeled)
  predX1 <- vector("list", 4)
  foreach(i = 1:4, .packages = "elmNN") %do% {
    x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
    y <- denoiseX1pretrain[[i]]$y
    SEED = 12345
    createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens  
    GetInputData(Ens = ens, X = x, Y = y) -> pred 
    return(list(ensemble = ens, pred = pred))
  } -> predX1
  names(predX1) <- group
}, env)  

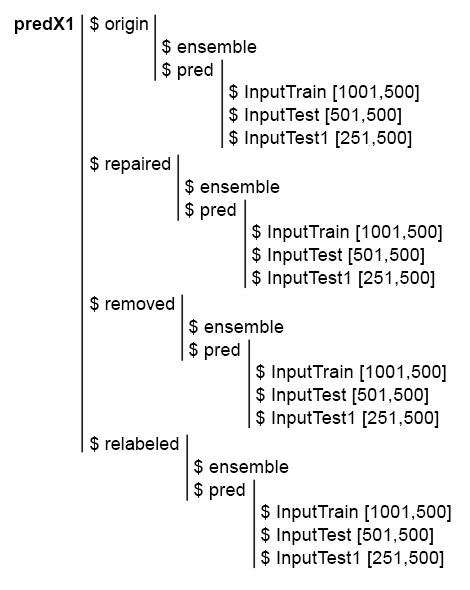
图例 6. predX1 集合的结构

请记住，要获得融合预测品质的度量，需要执行两项操作：修剪和平均（或简单多数表决）。 对于修剪，有必要将融合的每个神经网络的所有输出从连续形式转换为类标签。 然后定义每个神经网络的度量，并选择具有最佳得分的特定编号的神经网络。 然后平均这些最佳神经网络的连续预测并获得融合的连续平均预测。 再次，定义阈值，将平均预测转换为类标签，并计算融合的分类品质的最终得分。

因此，有必要将连续预测转换为类标签两次。 这两个阶段的转换阈值可以相同也可以不同。 哪些阈值变体可以使用？

1. 默认阈值。 在这种情况下，它等于 0.5。
2. 阈值等于中位数。 我认为它更可靠。 但中位数只能依据验证集合判断，即只能在测试后续子集合时才能应用。 例如，我们在 InputTrain 子集上定义阈值，稍后将在 InputTest 和 InputTest1 子集上使用这些阈值。
3. 针对各种标准优化阈值。 例如，它可以是最小分类误差，最大精度“1”或“0”等。 最佳阈值始终在 InputTrain 子集上确定，并在 InputTest 和 InputTest1 子集上使用。
4. 在对最佳神经网络的输出求平均值时，可以使用校准。 一些作者写道，只有经过良好校准的输出才能被平均。 确认此陈述超出了本文的范围。
   

最佳阈值可使用 InformationValue::optimalCutoff() 函数确定。 它在软件包中有详细描述。

若要确定 点 1 和点 2的阈值，不需要进行额外的计算。 若要计算点 3 的最佳阈值，我们编写函数 GetThreshold()。

#--function-------------------------
evalq({
  import_fun("InformationValue", optimalCutoff, CutOff)
  import_fun("InformationValue", youdensIndex, th_youdens)
  GetThreshold <- function(X, Y, type){
    switch(type,
           half = 0.5,
           med = median(X),
           mce = CutOff(Y, X, "misclasserror"),
           both = CutOff(Y, X,"Both"),
           ones = CutOff(Y, X, "Ones"),
           zeros = CutOff(Y, X, "Zeros")
    )
  }
}, env)

仅计算此函数中描述的前四种阈值（half，med，mce，both）。 前两个是 half 和 median 阈值。 mce 阈值提供最小分类误差，both 阈值 — 系数的最大值 youdensIndex = (sensitivity + specificity —1)。 计算顺序如下:

1. 在 predX1 集合中，依据 InputTrain 子集为融合的 500 个神经网络中的每一个计算四种类型的阈值，分别位于每组数据 (origin, repaired, removed 和 relabeled) 中。

2. 然后，使用这些阈值，将所有子集 (train|test|test1) 中的全部神经网络融合的连续预测转换为类，并确定平均值 F1。 我们获得四组度量，每组包含三个子集。 以下是 origin 组的分步脚本。

在 predX1$origin$pred$InputTrain 子集上定义 4 种类型的阈值:

#--threshold--train--origin--------
evalq({
  Ytest = X1$train$y
  Ytest1 = X1$test$y
  Ytest2 = X1$test1$y
  testX1 <- vector("list", 4)
  names(testX1) <- group
  type <- qc(half, med, mce, both)
  registerDoFuture()
  cl <- makeCluster(4)
  plan(cluster, workers = cl)
  foreach(i = 1:4, .combine = "cbind") %dopar% {# type
     foreach(j = 1:500, .combine = "c") %do% { 
        GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
     } 
  }  -> testX1$origin$Threshold
  stopCluster(cl)
  dimnames(testX1$origin$Threshold) <- list(NULL,type)
  }, env)

我们在每次计算中使用两个嵌套循环。 在外部循环中，选择阈值类型，创建集群，在 4 个核心上并行计算。 在内循环中，迭代融合的 500 个神经网络每一个的 InputTrain 预测。 为每一个定义 4 种类型的阈值。 所获数据的结构如下:

> env$testX1$origin$Threshold %>% str()
 num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
 - attr(*, "dimnames")=List of 2
  ..$ : NULL
  ..$ : chr [1:4] "half" "med" "mce" "both"
> env$testX1$origin$Threshold %>% head()
     half       med       mce      both
[1,]  0.5 0.5033552 0.3725180 0.5125180
[2,]  0.5 0.4918041 0.5118821 0.5118821
[3,]  0.5 0.5005034 0.5394191 0.5394191
[4,]  0.5 0.5138439 0.4764055 0.5164055
[5,]  0.5 0.5241393 0.5165478 0.5165478
[6,]  0.5 0.4673319 0.4508287 0.4608287

使用所获阈值，将子集 train, test 和 test1 的 origin 组的连续预测转换为类标签并计算度量 (mean(F1))。

#--train--------------------
evalq({
  foreach(i = 1:4, .combine = "cbind") %do% {# type
    foreach(j = 1:500, .combine = "c") %do% { 
      ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.; 
      Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
    }
  } -> testX1$origin$InputTrainScore
  dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
  foreach(i = 1:4, .combine = "cbind") %do% {# type
    foreach(j = 1:500, .combine = "c") %do% { 
      ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.; 
      Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
    }
  } -> testX1$origin$InputTestScore
  dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
  foreach(i = 1:4, .combine = "cbind") %do% {
    foreach(j = 1:500, .combine = "c") %do% { 
      ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.; 
      Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
    }
  } -> testX1$origin$InputTest1Score
  dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)

请参阅 origin 组及其三个子集的度量分布。 以下是 origin 组的脚本:

k <- 1L #origin
# k <- 2L #repaired
# k <- 3L #removed
# k <- 4L #relabeling
par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2))
boxplot(env$testX1[[k]]$Threshold, horizontal = F,
        main = paste0(env$group[k],"$$Threshold"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F,
        main = paste0(env$group[k],"$$InputTrainScore"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTestScore, horizontal = F,
        main = paste0(env$group[k],"$$InputTestScore"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F,
        main = paste0(env$group[k],"$$InputTest1Score"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
par(mfrow = c(1, 1))

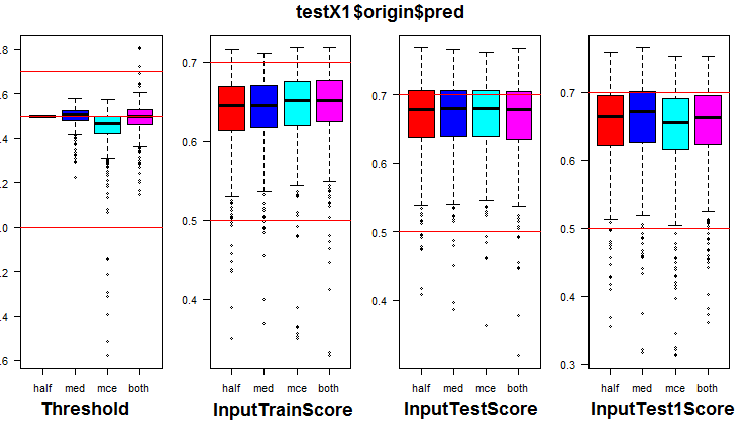
图例 7. 在 origin 组中阈值和度量的分布

直观显示，与“half”阈值相比，使用“med”作为 origin 数据组的阈值并未明显改善品质。

计算所有组中的所有 4 种类型的阈值（做好准备，它要花费大量的时间和内存）。

library("doFuture")
#--threshold--train---------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  type <- qc(half, med, mce, both)
  Ytest = X1$train$y
  Ytest1 = X1$test$y
  Ytest2 = X1$test1$y
  registerDoFuture()
  cl <- makeCluster(4)
  plan(cluster, workers = cl)
  while (k <= 4) { # group
    foreach(i = 1:4, .combine = "cbind") %dopar% {# type
      foreach(j = 1:500, .combine = "c") %do% { 
        GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i])
      } 
    }  -> testX1[[k]]$Threshold
    dimnames(testX1[[k]]$Threshold) <- list(NULL,type)
    k <- k + 1
  }
  stopCluster(cl)
}, env)

使用所获阈值，计算所有组和子集中的度量:

#--train--------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  while (k <= 4) {
    foreach(i = 1:4, .combine = "cbind") %do% {
      foreach(j = 1:500, .combine = "c") %do% { 
        ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; 
        Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
      }
    } -> testX1[[k]]$InputTrainScore
    dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type
    k <- k + 1
  }
}, env)
#--test-----------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  while (k <= 4) {
    foreach(i = 1:4, .combine = "cbind") %do% {
      foreach(j = 1:500, .combine = "c") %do% { 
        ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; 
        Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
      }
    } -> testX1[[k]]$InputTestScore
    dimnames(testX1[[k]]$InputTestScore)[[2]] <- type
    k <- k + 1
  }
}, env)
#--test1-----------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  while (k <= 4) {
    foreach(i = 1:4, .combine = "cbind") %do% {
      foreach(j = 1:500, .combine = "c") %do% { 
        ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; 
        Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
      }
    } -> testX1[[k]]$InputTest1Score
    dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type
    k <- k + 1
  }
}, env)

对于每组数据，我们添加了融合 500 个神经网络每一个依据三个子集上的四个不同阈值的度量。

我们来看看每个组和子集中度量是如何分布的。 该脚本是为 repaired 子集提供的。 它与其它组类似，只有组编号发生变化。 为清楚起见，所有组的图形将归拢到一幅图里显示。

# k <- 1L #origin
 k <- 2L #repaired
# k <- 3L #removed
# k <- 4L #relabeling
par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2))
boxplot(env$testX1[[k]]$Threshold, horizontal = F,
        main = paste0(env$group[k],"$$Threshold"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F,
        main = paste0(env$group[k],"$$InputTrainScore"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTestScore, horizontal = F,
        main = paste0(env$group[k],"$$InputTestScore"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F,
        main = paste0(env$group[k],"$$InputTest1Score"),
        col = c(2,4,5,6))
abline(h = c(0, 0.5, 0.7), col = 2)
par(mfrow = c(1, 1))

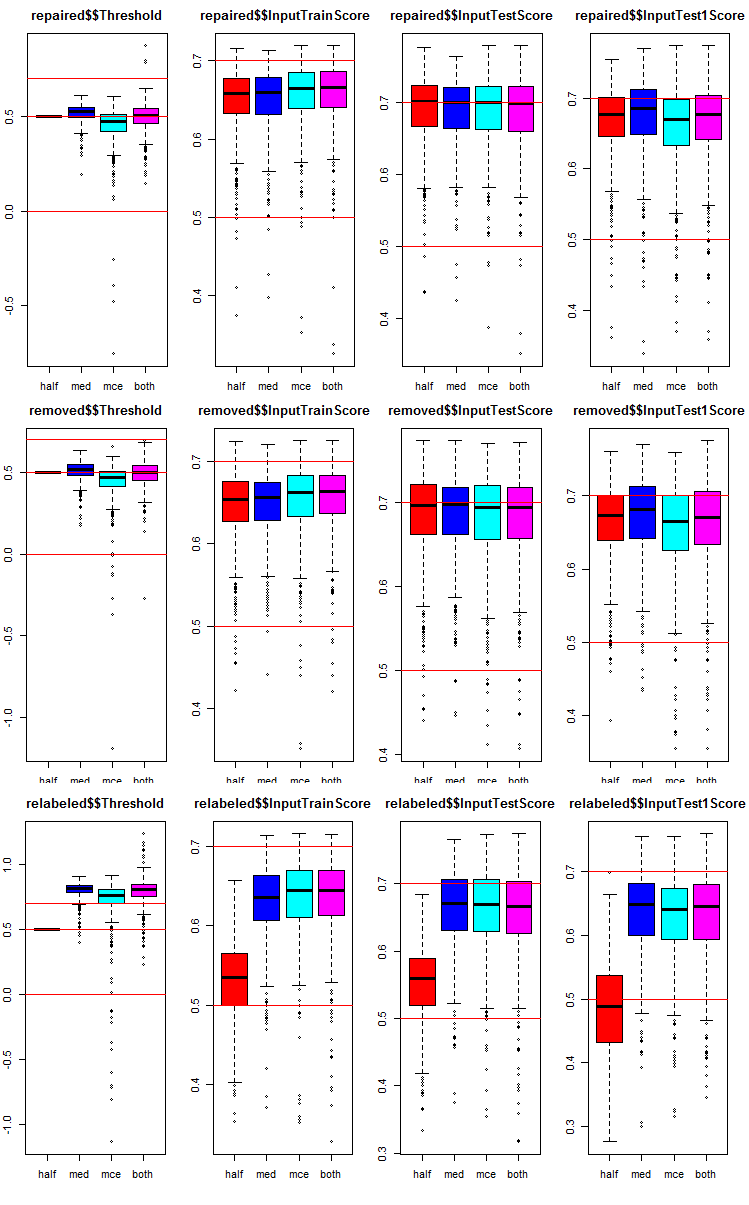
图例 8. 三个子集和四个不同阈值的三组数据中，融合的每个神经网络的预测度量分布图。

所有组都很通用:

• 测试子集的度量（InputTestScore）比验证子集的度量（InputTrainScore）要好得多;
• 第二个测试子集的度量（InputTest1Score）明显比第一个测试子集的度量更差;
• 类型“half”的阈值显示除了重新标记之外，所有子集上的结果都不比其它子集差。

本节中用到的所有脚本都可在 Threshold.R 文件中找到.

5. 测试融合

5.1. 在 InputTrain 子集中确定每个融合和每组数据中具有最佳度量的 7 个神经网络

进行修剪。 在 testX1 子集的每组数据中，有必要选择具有最大平均值 F1 的 7 个 InputTrainScore 值。 它们的索引将是融合中最佳的神经网络的索引。 该脚本如下所示，也可以在 Test.R 文件中找到。

#--bestNN----------------------------------------
evalq({
  nb <- 3L
  k <- 1L
while (k <= 4) {
  foreach(j = 1:4, .combine = "cbind") %do% {
    testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1)
  } -> testX1[[k]]$bestNN
  dimnames(testX1[[k]]$bestNN) <- list(NULL, type)
  k <- k + 1
  }
}, env)

我们获得了四组数据中的最佳得分的神经网络的索引 (origin, repaired, removed, relabeled)。 我们来深入研究它们，并根据数据组和阈值类型比较这些最佳神经网络的区别如何。

> env$testX1$origin$bestNN
     half med mce both
[1,]  415  75 415  415
[2,]  191 190 220  220
[3,]  469 220 191  191
[4,]  220 469 469  469
[5,]  265 287  57  444
[6,]  393 227 393   57
[7,]   75 322 444  393
> env$testX1$repaired$bestNN
     half med mce both
[1,]  393 393 154  154
[2,]  415  92 205  205
[3,]  205 154 220  220
[4,]  462 190 393  393
[5,]  435 392 287  287
[6,]  392 220  90   90
[7,]  265 287 415  415
> env$testX1$removed$bestNN
     half med mce both
[1,]  283 130 283  283
[2,]  207 110 300  300
[3,]  308 308 110  110
[4,]  159 134 192  130
[5,]  382 207 207  192
[6,]  192 283 130  308
[7,]  130 114 134  207
env$testX1$relabeled$bestNN
     half med mce both
[1,]  234 205 205  205
[2,]   69 287 469  469
[3,]  137 191 287  287
[4,]  269  57 191  191
[5,]  344 469 415  415
[6,]  164  75 444  444
[7,]  184 220  57   57

您可以看到具有“mce”和“both”阈值类型的神经网络的索引经常重合。

5.2. 这 7 个最佳神经网络的平均连续预测。

在选择 7 个最佳神经网络之后，在每组数据中，在子集 InputTrain，InputTest，InputTest1 和每个阈值类型中对它们进行平均。 用于处理 4 组中 InputTrain 子集的脚本:

#--Averaging--train------------------------
evalq({
  k <- 1L
  while (k <= 4) {# group
    foreach(j = 1:4, .combine = "cbind") %do% {# type
      bestNN <- testX1[[k]]$bestNN[ ,j]
      predX1[[k]]$pred$InputTrain[ ,bestNN] %>% 
        apply(1, function(x) sum(x)) %>% 
        divide_by((2*nb + 1))
    } -> testX1[[k]]$TrainYpred
    dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type))
    k <- k + 1
  }
}, env)

我们看一下在 repaired 数据组中所获的平均连续预测的结构和统计得分：

> env$testX1$repaired$TrainYpred %>% str()
 num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ...
 - attr(*, "dimnames")=List of 2
  ..$ : NULL
  ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both"
> env$testX1$repaired$TrainYpred %>% summary()
  Y.aver_half        Y.aver_med        Y.aver_mce       Y.aver_both     
 Min.   :-0.2202   Min.   :-0.4021   Min.   :-0.4106   Min.   :-0.4106  
 1st Qu.: 0.3348   1st Qu.: 0.3530   1st Qu.: 0.3512   1st Qu.: 0.3512  
 Median : 0.5323   Median : 0.5462   Median : 0.5462   Median : 0.5462  
 Mean   : 0.5172   Mean   : 0.5010   Mean   : 0.5012   Mean   : 0.5012  
 3rd Qu.: 0.7227   3rd Qu.: 0.7153   3rd Qu.: 0.7111   3rd Qu.: 0.7111  
 Max.   : 1.1874   Max.   : 1.0813   Max.   : 1.1039   Max.   : 1.1039

最后两种阈值类型的统计数据也是相同的。 以下是其余两个子集 InputTest，InputTest1 的脚本:

#--Averaging--test------------------------
evalq({
  k <- 1L
  while (k <= 4) {# group
    foreach(j = 1:4, .combine = "cbind") %do% {# type
      bestNN <- testX1[[k]]$bestNN[ ,j]
      predX1[[k]]$pred$InputTest[ ,bestNN] %>% 
        apply(1, function(x) sum(x)) %>% 
        divide_by((2*nb + 1))
    } -> testX1[[k]]$TestYpred
    dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type))
    k <- k + 1
  }
}, env)
#--Averaging--test1------------------------
evalq({
  k <- 1L
  while (k <= 4) {# group
    foreach(j = 1:4, .combine = "cbind") %do% {# type
      bestNN <- testX1[[k]]$bestNN[ ,j]
      predX1[[k]]$pred$InputTest1[ ,bestNN] %>% 
        apply(1, function(x) sum(x)) %>% 
        divide_by((2*nb + 1))
    } -> testX1[[k]]$Test1Ypred
    dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type))
    k <- k + 1
  }
}, env)

我们看一下 repaired 数据组的 InputTest 子集的统计信息:

> env$testX1$repaired$TestYpred %>% summary()
  Y.aver_half        Y.aver_med        Y.aver_mce       Y.aver_both     
 Min.   :-0.1524   Min.   :-0.5055   Min.   :-0.5044   Min.   :-0.5044  
 1st Qu.: 0.2888   1st Qu.: 0.3276   1st Qu.: 0.3122   1st Qu.: 0.3122  
 Median : 0.5177   Median : 0.5231   Median : 0.5134   Median : 0.5134  
 Mean   : 0.5114   Mean   : 0.4976   Mean   : 0.4946   Mean   : 0.4946  
 3rd Qu.: 0.7466   3rd Qu.: 0.7116   3rd Qu.: 0.7149   3rd Qu.: 0.7149  
 Max.   : 1.1978   Max.   : 1.0428   Max.   : 1.0722   Max.   : 1.0722  

最后两种阈值类型的统计数据也是相同的。

5.3. 定义平均连续预测的阈值

现在我们对每个融合进行了平均预测。 需要将它们转换为类标签，以及所有数据组和阈值类型的最终品质度量。 为此，与之前的计算类似，仅使用 InputTrain 子集确定最佳阈值。 下面提供的脚本计算每个组和每个子集中的阈值:

#-th_aver------------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  type <- qc(half, med, mce, both)
  Ytest = X1$train$y
  Ytest1 = X1$test$y
  Ytest2 = X1$test1$y
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type subset
      foreach(i = 1:4, .combine = "c") %do% {# type threshold
        GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i])
      } 
    }  -> testX1[[k]]$th_aver
    dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred))
    k <- k + 1
  }
}, env)

5.4. 将融合的平均连续预测转换为类标签，并计算所有数据组 InputTrain，InputTest 和 InputTest1 子集上的融合度量。

使用上面计算的 th_aver 阈值，确定度量:

#---Metrics--train-------------------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type subset
      foreach(i = 1:4, .combine = "c") %do% {# type threshold
        ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver
        Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>%
          mean() %>% round(3)
      } 
    }  -> testX1[[k]]$TrainScore
    dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred))
    k <- k + 1
  }
}, env)
#---Metrics--test-------------------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type subset
      foreach(i = 1:4, .combine = "c") %do% {# type threshold
        ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver
        Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>%
          mean() %>% round(3)
      } 
    }  -> testX1[[k]]$TestScore
    dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred))
    k <- k + 1
  }
}, env)
#---Metrics--test1-------------------------------------
evalq({
  k <- 1L #origin
  #k <- 2L #repaired
  #k <- 3L #removed
  #k <- 4L #relabeling
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type subset
      foreach(i = 1:4, .combine = "c") %do% {# type threshold
        ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver
        Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>%
          mean() %>% round(3)
      } 
    }  -> testX1[[k]]$Test1Score
    dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred))
    k <- k + 1
  }
}, env)

创建汇总表格并分析所获度量。 我们从 origin 组开始（它的噪声样本未用任何方式处理）。 我们正在寻找 TestScore 和 Test1Score 的得分。 TestTrain 子集的得分是指示性的，需要将它们与测试得分进行比较:

> env$testX1$origin$TrainScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.711      0.708      0.712       0.712
med        0.711      0.713      0.707       0.707
mce        0.712      0.704      0.717       0.717
both       0.711      0.706      0.717       0.717
> env$testX1$origin$TestScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.750      0.738      0.745       0.745
med        0.748      0.742      0.746       0.746
mce        0.742      0.720      0.747       0.747
both       0.748      0.730      0.747       0.747
> env$testX1$origin$Test1Score
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.735      0.732      0.716       0.716
med        0.733      0.753      0.745       0.745
mce        0.735      0.717      0.716       0.716
both       0.733      0.750      0.716       0.716

拟议的表格示意出什么？

在两种变换中（修剪和平均），在 TestScore 中“half”阈值的变体展示出最佳结果 0.750。 然而，Test1Score 子集中的品质下降到 0.735。

当修剪和平均时，两个子集中阈值变体（med，mce，both） 展示更稳定的结果 ~0.745。

查看下一组数据 — repaired（含有已矫正噪声样本标签）:

> env$testX1$repaired$TrainScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.713      0.711      0.717       0.717
med        0.709      0.709      0.713       0.713
mce        0.728      0.714      0.709       0.709
both       0.728      0.711      0.717       0.717
> env$testX1$repaired$TestScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.759      0.761      0.756       0.756
med        0.754      0.748      0.747       0.747
mce        0.758      0.755      0.743       0.743
both       0.758      0.732      0.754       0.754
> env$testX1$repaired$Test1Score
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.719      0.744      0.724       0.724
med        0.738      0.748      0.744       0.744
mce        0.697      0.720      0.677       0.677
both       0.697      0.743      0.731       0.731

表中显示的最佳结果是 half/half 组合中的 0.759。 当修剪时，两个子集中阈值变体（half，mce，both） 展示更稳定的结果 ~0.750，当平均时为 med。

请参阅下一个数据组 — removed (将噪声样本从集合中移除):

> env$testX1$removed$TrainScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.713      0.720      0.724       0.718
med        0.715      0.717      0.715       0.717
mce        0.721      0.722      0.725       0.723
both       0.721      0.720      0.725       0.723
> env$testX1$removed$TestScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.761      0.769      0.761       0.751
med        0.752      0.749      0.760       0.752
mce        0.749      0.755      0.753       0.737
both       0.749      0.736      0.753       0.760
> env$testX1$removed$Test1Score
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.712      0.732      0.716       0.720
med        0.729      0.748      0.740       0.736
mce        0.685      0.724      0.721       0.685
both       0.685      0.755      0.721       0.733

分析表格。 在 TestScore 中 med/half 阈值变体展示出最佳结果 0.769。 不过，Test1Score 子集的品质下降到 0.732。 对于 TestScore 子集，当修剪时（half，med，mce，both）的最佳组合，以及当平均时阈值的一半产生所有组的最佳得分。

查看最后一个数据组 — relabeled (将噪声样本隔离到一个单独的类中):

> env$testX1$relabeled$TrainScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.672      0.559      0.529       0.529
med        0.715      0.715      0.711       0.711
mce        0.712      0.715      0.717       0.717
both       0.710      0.718      0.720       0.720
> env$testX1$relabeled$TestScore
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.719      0.572      0.555       0.555
med        0.736      0.748      0.746       0.746
mce        0.739      0.747      0.745       0.745
both       0.710      0.756      0.754       0.754
> env$testX1$relabeled$Test1Score
     Y.aver_half Y.aver_med Y.aver_mce Y.aver_both
half       0.664      0.498      0.466       0.466
med        0.721      0.748      0.740       0.740
mce        0.739      0.732      0.716       0.716
both       0.734      0.737      0.735       0.735

该组的最佳结果是通过以下阈值组合产生的：当修剪时，（med，mce，both），当平均时，both or med。

下图显示上述所有计算后 testX1 的数据结构:

图例 9. testX1 的数据结构。

6. 优化神经网络分类器融合的超参数

所有先前的计算都是基于个人经验设置，并在具有相同神经网络超参数的融合上进行的。 您可能知道，与其它模型一样，神经网络的超参数需要针对特定数据集合进行优化，以便获得更好的结果。 对于训练，我们将去噪数据分为 4 组 (origin, repaired, removed 和 relabeled)。 因此，有必要为这些融合的神经网络获取精确的最优超参数。 有关贝叶斯优化的所有问题已在 前一篇文章 中进行了详细讨论，因此这里不再赘述。

将优化神经网络得 4 个超参数:

• 预测因子的数量 — numFeature = c(3L, 13L) 范围从 3 至 13;
• 训练中使用的样本百分比 — r = c(1L, 10L) 范围从 10 % 至 100%;
• 隐藏层中的神经元数量 — nh = c(1L, 51L) 范围从 1 至 51;
• 激活函数的类型 — fact = c(1L, 10L) 激活函数列表中的索引 Fact.

设置常量:

##===OPTIM===============================
evalq({
  #type of activation function. 
  Fact <- c("sig", #: sigmoid
            "sin", #: sine
            "radbas", #: radial basis
            "hardlim", #: hard-limit
            "hardlims", #: symmetric hard-limit
            "satlins", #: satlins
            "tansig", #: tan-sigmoid
            "tribas", #: triangular basis
            "poslin", #: positive linear
            "purelin") #: linear
  bonds <- list(
    numFeature = c(3L, 13L),
    r = c(1L, 10L),
    nh = c(1L, 51L),
    fact = c(1L, 10L)
  )
}, env)

编写一个 fitness 函数，它将返回品质指标 Score = mean(F1) 和融合预测的类标签。 将使用相同的 threshold = 0.5，针对修剪（在融合中选择最佳神经网络）和平均进行连续预测。 事实证明它是一个非常好的选择 — 至少对于第一次逼近。 脚本如下:

#---Fitnes -FUN-----------
evalq({
  n <- 500
  numEns <- 3
  # SEED <- c(12345, 1235809)
  fitnes <- function(numFeature, r, nh, fact){
    bestF <- orderX %>% head(numFeature)
    k <- 1
    rng <- RNGseq(n, SEED)
    #---train---
    Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
      k <- k + 1
      elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], 
               nhid = nh, actfun = Fact[fact])
    }
    #---predict---
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest[ , bestF])
    } -> y.pr #[ ,n]
    #---best---
    foreach(i = 1:n, .combine = "c") %do% {
      ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
      Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
        mean() 
    } -> Score
    Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
    #---test-aver--------
    foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
      when(i %in% bestNN) %do% {
        predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>%
      divide_by(length(bestNN)) -> ensPred
    ifelse(ensPred > 0.5, 1, 0) -> ensPred
    Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>%
      mean() %>% round(3) -> Score
    return(list(Score = Score, Pred = ensPred))
  }
}, env)  

已注释 SEED 变量有两个数值。 必须检查此参数对结果实验的影响。 我已用相同的初始数据和参数执行了优化，但使用了两个不同的 SEED 值。 SEED = 1235809 展示出最好的结果。 该值将在下面的脚本中使用。 但会为 SEED 的两个值提供所获得的超参数和分类品质得分。 您可以尝试其它数值。

我们检查 fitness 函数是否工作，一次计算要经历多长时间并查看结果:

evalq({
   Ytrain <- X1$pretrain$y
   Ytest <- X1$train$y
   Ytest1 <- X1$test$y
   Xtrain <- X1$pretrain$x
   Xtest <- X1$train$x
   Xtest1 <- X1$test$x 
   orderX <- orderX1
   SEED <- 1235809
  system.time(
    res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
  )
 }, env)
user  system elapsed 
   5.89    0.00    5.99 
env$res$Score
[1] 0.741

以下脚本针对去噪数据的每一组连续优化神经网络超参数。 使用起始随机初始化 20 个点，及 20 次后续迭代。 

#---Optim Ensemble-----
library(rBayesianOptimization)
evalq({
  Ytest <- X1$train$y
  Ytest1 <- X1$test$y
  Xtest <- X1$train$x
  Xtest1 <- X1$test$x 
  orderX <- orderX1
  SEED <- 1235809
  OPT_Res <- vector("list", 4)
  foreach(i = 1:4) %do% {
    Xtrain <- denoiseX1pretrain[[i]]$x
    Ytrain <- denoiseX1pretrain[[i]]$y
    BayesianOptimization(fitnes, bounds = bonds,
                                  init_grid_dt = NULL, init_points = 20, 
                                  n_iter = 20, acq = "ucb", kappa = 2.576, 
                                  eps = 0.0, verbose = TRUE,
                                  maxit = 100, control = c(100, 50, 8))
  } -> OPT_Res1
  group <- qc(origin, repaired, removed, relabeled)
  names(OPT_Res1) <- group
}, env)

一旦您开始执行脚本，请耐心等待大约半小时（这取决于您的硬件）。 按降序对获得的得分值进行排序，并选择三个最佳得分。 这些得分会分配给变量 best.res（对于 SEED = 12345），和 best.res1（对于 SEED = 1235809）。 

#---OptPar------
evalq({
  foreach(i = 1:4) %do% {
    OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
  } -> best.res
  names(best.res) <- group
}, env)
evalq({
  foreach(i = 1:4) %do% {
     OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
  } -> best.res1
  names(best.res1) <- group
}, env)

查看 best.res 分数:

env$best.res
# $origin
#    Round numFeature r nh fact Value
# 1     39         10 7 20    2 0.769
# 2     12          6 4 38    2 0.766
# 3     38          4 3 15    2 0.766

# 
# $repaired
#    Round numFeature  r nh fact Value
# 1      5         10  5 20    7 0.767
# 2      7          5  2 36    9 0.766
# 3     28          5 10  6    8 0.766

# 
# $removed
#    Round numFeature  r nh fact Value
# 1      1         11  6 44    9 0.764
# 2      8          8  6 26    7 0.764
# 3     19         12  1 40    5 0.763

# 
# $relabeled
#    Round numFeature  r nh fact Value
# 1     24          9 10  1   10 0.746
# 2      7          9  9  2    8 0.745
# 3     32          4  1  1   10 0.738

对于 best.res1 分数相同:

> env$best.res1
$origin
  Round numFeature r nh fact Value
1    19          8 3 41    2 0.777
2    32          8 1 33    2 0.777
3    23          6 1 35    1 0.770

$repaired
  Round numFeature r nh fact Value
1    26          9 4 17    3 0.772
2    33         11 9 30    9 0.771
3    38          5 4 17    2 0.770

$removed
  Round numFeature r nh fact Value
1    30          5 4 17    2 0.770
2     8          8 2 13    6 0.769
3    32          5 3 22    7 0.766

$relabeled
  Round numFeature r nh fact Value
1    34         12 5  8    9 0.777
2    33          9 5  4    9 0.763
3    36         12 7  4    9 0.760

如您所见，这些结果看起来更好。 相比之下，您不光能输出前三个结果，而是十个：差异将更加明显。 

我们为 4 个数据组收集融合得神经网络的最佳超参数。 稍后将需要它们来创建具有最佳超参数的融合。

#---best.param-------------------
evalq({
  foreach(i = 1:4, .combine = "rbind") %do% {
    OPT_Res1[[i]]$Best_Par %>% unname()
  } -> best.par1
  dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)

超参数:

> env$best.par1
          numFeature r nh fact
origin             8 3 41    2
repaired           9 4 17    3
removed            5 4 17    2
relabeled         12 5  8    9

此脚本中的所有脚本都可在 Optim_VIII.R 文件中找到。

7. 优化后期处理超参数（修剪和平均的阈值）

神经网络超参数的优化提供了分类品质的小幅提升。 如前所述，修剪和平均时阈值类型的组合对分类品质的影响更大。 

我们已经使用阈值的一半/一半的恒定组合优化了超参数。 也许这种组合不是最佳的。 我们用两个额外的优化参数重复优化 th1 = c(1L, 2L)) — 修剪融合时的阈值类型（选择最佳神经网络） — 和 th2 = c(1L, 4L) — 将融合的平均预测转换为类标签时的阈值类型。 定义要优化的超参数的常量和取值范围。

##===OPTIM===============================
evalq({
  #type of activation function. 
  Fact <- c("sig", #: sigmoid
            "sin", #: sine
            "radbas", #: radial basis
            "hardlim", #: hard-limit
            "hardlims", #: symmetric hard-limit
            "satlins", #: satlins
            "tansig", #: tan-sigmoid
            "tribas", #: triangular basis
            "poslin", #: positive linear
            "purelin") #: linear
  bonds_m <- list(
    numFeature = c(3L, 13L),
    r = c(1L, 10L),
    nh = c(1L, 51L),
    fact = c(1L, 10L),
    th1 = c(1L, 2L),
    th2 = c(1L, 4L)
  )
}, env)

关于 fitness 函数。 稍作修改：添加了两个形式参数 th1，th2。 在函数实体和 'best' 模块中，根据 th1 计算阈值。 在 'test-average' 模块中，根据阈值类型 th2 使用 GetThreshold() 函数确定阈值。

#---Fitnes -FUN-----------
evalq({
  n <- 500L
  numEns <- 3L
  # SEED <- c(12345, 1235809)
  fitnes_m <- function(numFeature, r, nh, fact, th1, th2){
    bestF <- orderX %>% head(numFeature)
    k <- 1L
    rng <- RNGseq(n, SEED)
    #---train---
    Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
      k <- k + 1
      elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], 
               nhid = nh, actfun = Fact[fact])
    }
    #---predict---
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest[ , bestF])
    } -> y.pr #[ ,n]
    #---best---
    ifelse(th1 == 1L, 0.5, median(y.pr)) -> th
    foreach(i = 1:n, .combine = "c") %do% {
      ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred
      Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
        mean() 
    } -> Score
    Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
    #---test-aver--------
    foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
      when(i %in% bestNN) %do% {
        predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>%
      divide_by(length(bestNN)) -> ensPred
    th <- GetThreshold(ensPred, Yts$Ytest1, type[th2])
    ifelse(ensPred > th, 1, 0) -> ensPred
    Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>%
      mean() %>% round(3) -> Score
    return(list(Score = Score, Pred = ensPred))
  }
}, env) 

检查此函数迭代一次需要多长时间以及它是否工作:

#---res fitnes-------
evalq({
  Ytrain <- X1$pretrain$y
  Ytest <- X1$train$y
  Ytest1 <- X1$test$y
  Xtrain <- X1$pretrain$x
  Xtest <- X1$train$x
  Xtest1 <- X1$test$x 
  orderX <- orderX1
  SEED <- 1235809
  th1 <- 1
  th2 <- 4
  system.time(
    res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2)
  )
}, env)
   user  system elapsed 
   6.13    0.04    6.32 
> env$res_m$Score
[1] 0.748

函数的执行时间变化不大。 之后，运行优化并等待结果:

#---Optim Ensemble-----
library(rBayesianOptimization)
evalq({
  Ytest <- X1$train$y
  Ytest1 <- X1$test$y
  Xtest <- X1$train$x
  Xtest1 <- X1$test$x 
  orderX <- orderX1
  SEED <- 1235809
  OPT_Res1 <- vector("list", 4)
  foreach(i = 1:4) %do% {
    Xtrain <- denoiseX1pretrain[[i]]$x
    Ytrain <- denoiseX1pretrain[[i]]$y
    BayesianOptimization(fitnes_m, bounds = bonds_m,
                         init_grid_dt = NULL, init_points = 20, 
                         n_iter = 20, acq = "ucb", kappa = 2.576, 
                         eps = 0.0, verbose = TRUE,
                         maxit = 100) #, control = c(100, 50, 8))
  } -> OPT_Res_m
  group <- qc(origin, repaired, removed, relabeled)
  names(OPT_Res_m) <- group
}, env)

为每组数据选择 10 个获取的最佳超参数:

#---OptPar------
evalq({
  foreach(i = 1:4) %do% {
    OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
  } -> best.res_m
  names(best.res_m) <- group
}, env)
$origin
   Round numFeature  r nh fact th1 th2 Value
1     19          8  3 41    2   2   4 0.778
2     25          6  8 51    8   2   4 0.778
3     39          9  1 22    1   2   4 0.777
4     32          8  1 21    2   2   4 0.772
5     10          6  5 32    3   1   3 0.769
6     22          7  2 30    9   1   4 0.769
7     28          6 10 25    5   1   4 0.769
8     30          7  9 33    2   2   4 0.768
9     40          9  2 48   10   2   4 0.768
10    23          9  1  2   10   2   4 0.767

$repaired
   Round numFeature  r nh fact th1 th2 Value
1     39          7  8 39    8   1   4 0.782
2      2          5  8 50    3   2   3 0.775
3      3         12  6  7    8   1   1 0.769
4     24          5 10 45    5   2   3 0.769
5     10          7  8 40    2   1   4 0.768
6     13          5  8 40    2   2   4 0.768
7      9          6  9 13    2   2   3 0.766
8     19          5  7 46    6   2   1 0.765
9     40          9  8 50    6   1   4 0.764
10    20          9  3 28    9   1   3 0.763

$removed
   Round numFeature  r nh fact th1 th2 Value
1     40          7  2 39    8   1   3 0.786
2     13          5  3 48    3   2   3 0.776
3      8          5  6 18    1   1   1 0.772
4      5          5 10 24    3   1   3 0.771
5     29         13  7  1    1   1   4 0.771
6      9          7  3 25    7   1   4 0.770
7     17          9  2 17    1   1   4 0.770
8     19          7  7 25    2   1   3 0.768
9      4         10  6 19    7   1   3 0.765
10     2          4  4 47    7   2   3 0.764

$relabeled
   Round numFeature  r nh fact th1 th2 Value
1      7          8  1 13    1   2   4 0.778
2     26          8  1 19    6   2   4 0.768
3      3          6  3 45    4   2   2 0.766
4     20          6  2 40   10   2   2 0.766
5     13          4  3 18    2   2   3 0.762
6     10         10  6  4    8   1   3 0.761
7     31         11 10 16    1   2   4 0.760
8     15         13  7  7    1   2   3 0.759
9      5          7  3 20    2   1   4 0.758
10     9          9  3 22    8   2   3 0.758

品质略有改善。 每组数据的最佳超参数与先前优化期间不考虑阈值不同组合所获得的超参数有很大不同。 数据组通过重新标记 (repaired) 和删除 (removed) 噪声样本来证明最佳品质得分。

#---best.param-------------------
evalq({
  foreach(i = 1:4, .combine = "rbind") %do% {
    OPT_Res_m[[i]]$Best_Par %>% unname()
  } -> best.par_m
  dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2))
}, env)
# > env$best.par_m------------------------
#           numFeature r nh fact th1 th2
# origin             8 3 41    2   2   4
# repaired           7 8 39    8   1   4
# removed            7 2 39    8   1   3
# relabeled          8 1 13    1   2   4

本节中使用的脚本位于 Optim_mVIII.R 文件中。

8. 将若干最佳融合组合成一个超级融合，还有它们的输出

将若干最好的融合组合成一个超级融合，它们的输出通过简单多数表决级联。

首先，将优化过程中获得的若干最佳融合的结果组合到一起。 在优化之后，该函数不仅返回最佳超参数，还返回所有迭代中类标签中的预测历史。 由每组数据中的 5 个最佳融合生成超级集合，并使用简单多数表决来检查该变体中的分类品质得分是否有所改善。 

计算按以下顺序进行:

• 在一次循环中顺序迭代 4 组数据;
• 确定每组数据中 5 个最佳预测的索引;
• 将索引指向得预测结合到一个数据帧中;
• 在所有预测中将类标签从“0”更改为“-1”;
• 将这些预测一行一行地加以汇总;
• 根据条件将这些汇总数值转换为类标签（-1,0,1）: 如果该值大于 3，则 class = 1; 如果小于 -3，则class = -1; 否则 class = 0 

此为执行这些计算的脚本:

#--Index-best-------------------
evalq({
  prVot <- vector("list", 4)
  foreach(i = 1:4) %do% { #group
    best.res_m[[i]]$Round %>% head(5) -> ind 
    OPT_Res_m[[i]]$Pred  %>% dp$select(ind)  ->.; 
    apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.; 
    apply(., 1, function(x) sum(x)) ->.; 
    ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
 } -> prVot
  names(prVot) <- group
}, env)

我们还有一个额外的第三类“0”。 如果为“-1”，则为“卖出”，“1”为“买入”，“0”为“不确定”。 智能交易系统如何对此信号作出反应则取决于用户。 它可以远离市场，也可以在市场上无所事事，等待新的信号发挥作用。 在测试智能系统时，应该构建并检查行为模型。 

若要获得度量，则必须:

• 在一次循环中顺序迭代每组数据;
• 在目标 Ytest1 的实际值中，将“0”类标签替换为标签“-1”;
• 将实际和上面获得的预测目标 prVot 组合成数据帧;
• 从数据帧中将值为 prVot = 0 的行删除;
• 计算度量。

计算并查看结果。

evalq({
  foreach(i = 1:4) %do% { #group
   Ytest1  ->.; 
    ifelse(. == 0, -1, 1) ->.; 
    cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.; 
    dp$filter(., pred != 0) -> tabl
    Eval(tabl$actual, tabl$pred)
  } -> Score
  names(Score) <- group
}, env) 
env$Score
$origin
$origin$metrics
   Accuracy Precision Recall    F1
-1    0.806     0.809  0.762 0.785
1     0.806     0.804  0.845 0.824

$origin$confMatr
Confusion Matrix and Statistics

      predicted
actual  -1   1
    -1 157  49
    1   37 201
                                         
               Accuracy : 0.8063         
                 95% CI : (0.7664, 0.842)
    No Information Rate : 0.5631         
    P-Value [Acc > NIR] : <2e-16         
                                         
                  Kappa : 0.6091         
 Mcnemar's Test P-Value : 0.2356         
                                         
            Sensitivity : 0.8093         
            Specificity : 0.8040         
         Pos Pred Value : 0.7621         
         Neg Pred Value : 0.8445         
             Prevalence : 0.4369         
         Detection Rate : 0.3536         
   Detection Prevalence : 0.4640         
      Balanced Accuracy : 0.8066         
                                         
       'Positive' Class : -1             
                                         


$repaired
$repaired$metrics
   Accuracy Precision Recall    F1
-1     0.82     0.826  0.770 0.797
1      0.82     0.816  0.863 0.839

$repaired$confMatr
Confusion Matrix and Statistics

      predicted
actual  -1   1
    -1 147  44
    1   31 195
                                          
               Accuracy : 0.8201          
                 95% CI : (0.7798, 0.8558)
    No Information Rate : 0.5731          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.6358          
 Mcnemar's Test P-Value : 0.1659          
                                          
            Sensitivity : 0.8258          
            Specificity : 0.8159          
         Pos Pred Value : 0.7696          
         Neg Pred Value : 0.8628          
             Prevalence : 0.4269          
         Detection Rate : 0.3525          
   Detection Prevalence : 0.4580          
      Balanced Accuracy : 0.8209          
                                          
       'Positive' Class : -1              
                                          


$removed
$removed$metrics
   Accuracy Precision Recall    F1
-1    0.819     0.843  0.740 0.788
1     0.819     0.802  0.885 0.841

$removed$confMatr
Confusion Matrix and Statistics

      predicted
actual  -1   1
    -1 145  51
    1   27 207
                                          
               Accuracy : 0.8186          
                 95% CI : (0.7789, 0.8539)
    No Information Rate : 0.6             
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.6307          
 Mcnemar's Test P-Value : 0.009208        
                                          
            Sensitivity : 0.8430          
            Specificity : 0.8023          
         Pos Pred Value : 0.7398          
         Neg Pred Value : 0.8846          
             Prevalence : 0.4000          
         Detection Rate : 0.3372          
   Detection Prevalence : 0.4558          
      Balanced Accuracy : 0.8227          
                                          
       'Positive' Class : -1              
                                          


$relabeled
$relabeled$metrics
   Accuracy Precision Recall    F1
-1    0.815     0.809  0.801 0.805
1     0.815     0.820  0.828 0.824

$relabeled$confMatr
Confusion Matrix and Statistics

      predicted
actual  -1   1
    -1 157  39
    1   37 178
                                          
               Accuracy : 0.8151          
                 95% CI : (0.7741, 0.8515)
    No Information Rate : 0.528           
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.6292          
 Mcnemar's Test P-Value : 0.9087          
                                          
            Sensitivity : 0.8093          
            Specificity : 0.8203          
         Pos Pred Value : 0.8010          
         Neg Pred Value : 0.8279          
             Prevalence : 0.4720          
         Detection Rate : 0.3820          
   Detection Prevalence : 0.4769          
      Balanced Accuracy : 0.8148          
                                          
       'Positive' Class : -1   
#---------------------------------------

所有组的品质都有显著提高。 已经在 removed (0.8227) 和 repaired (0.8209) 组中获得了 'Balanced Accuracy' 的最佳得分。                                        

我们还使用简单多数表决组合组预测。 执行组合级联:

• 在一次循环中迭代所有数据组;
• 确定最佳结果的轮试索引;
• 选择这些最佳轮试的预测;
• 在每列中，将标签“0”替换为标签“-1”;
• 逐行汇总组中的预测。
  

查看获得的结果:

#--Index-best-------------------
evalq({
  foreach(i = 1:4, .combine = "+") %do% { #group
    best.res_m[[i]]$Round %>% head(5) -> ind 
    OPT_Res_m[[i]]$Pred  %>% dp$select(ind)  ->.; 
    apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.; 
    apply(., 1, function(x) sum(x)) 
 } -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10  -8  -6  -4  -2   0   2   4   6   8  10  12  14  16  18  20 
166  12   4   6   7   6   5   3   6   1   4   4   5   6   5  10   7   3   8  24 209

仅保留最大的表决值并计算度量:

evalq({
    pred <- {prVotSum ->.; 
       ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
    Ytest1  ->.; 
    ifelse(. == 0, -1, 1) ->.; 
    cbind(actual = ., pred = pred) %>% as.data.frame() ->.; 
    dp$filter(., pred != 0) -> tabl
    Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env) 
env$ScoreSum
> env$ScoreSum
$metrics
   Accuracy Precision Recall    F1
-1    0.835     0.849  0.792 0.820
1     0.835     0.823  0.873 0.847

$confMatr
Confusion Matrix and Statistics

      predicted
actual  -1   1
    -1 141  37
    1   25 172
                                          
               Accuracy : 0.8347          
                 95% CI : (0.7931, 0.8708)
    No Information Rate : 0.5573          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.6674          
 Mcnemar's Test P-Value : 0.1624          
                                          
            Sensitivity : 0.8494          
            Specificity : 0.8230          
         Pos Pred Value : 0.7921          
         Neg Pred Value : 0.8731          
             Prevalence : 0.4427          
         Detection Rate : 0.3760          
   Detection Prevalence : 0.4747          
      Balanced Accuracy : 0.8362          
                                          
       'Positive' Class : -1    

这产生了非常好的 Balanced Accuracy = 0.8362。

本节中描述的脚本位于 Voting.R 文件中。

但我们不能忘记一个细微差别。 在优化超参数时，我们使用了 InputTest 测试集合。 这意味着我们可以开始使用下一个测试集合 InputTest1。 在不优化超参数的情况下，在级联的融合组合中最有可能产生相同的正面效果。 在先前获得的平均结果上查验它。

结合 5.2 节中所获融合的平均输出。 

重现 5.4 节中描述的计算，只需更改一处。 当连续平均预测转换为类标签时, 这些标签将是 [-1, 0, 1]。 在每个子集 train/test/test1 中的计算顺序:

• 在一次循环中顺序迭代 4 组数据;
• 通过 4 种类型的修剪阈值;
• 通过 4 种类型的平均阈值;
• 将融合的连续平均预测转换为类标签 [-1,1];
• 将它们与 4 种平均阈值相加;
• 总和重新标记为新标签 [-1,0,1];
  
• 将获得的结果添加到 VotAver 结构中。
  

#---train-------------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  VotAver <- vector("list", 4)
  names(VotAver) <- group
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type aver
      foreach(i = 1:4, .combine = "+") %do% {# type threshold
        ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1)
      } ->.; 
      ifelse(. > 2, 1, ifelse(. < -2, -1, 0))  
    }  -> VotAver[[k]]$Train.clVoting
    dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type)
    k <- k + 1
  }
}, env)
#---test------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type aver
      foreach(i = 1:4, .combine = "+") %do% {# type threshold
        ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1)
      } ->.; 
      ifelse(. > 2, 1, ifelse(. < -2, -1, 0))  
    }  -> VotAver[[k]]$Test.clVoting
    dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type)
    k <- k + 1
  }
}, env)
#---test1-------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(j = 1:4, .combine = "cbind") %do% {# type aver
      foreach(i = 1:4, .combine = "+") %do% {# type threshold
        ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1)
      } ->.; 
      ifelse(. > 2, 1, ifelse(. < -2, -1, 0))  
    }  -> VotAver[[k]]$Test1.clVoting
    dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type)
    k <- k + 1
  }
}, env)

一旦确定子集和数据组中重新标记的平均预测后，计算它们的度量。 计算顺序:

• 在一次循环中迭代数据组;
• 迭代平均阈值的 4 种类型;
• 在实际预测中将类标签从“0”更改为“-1”;
• 将实际和重标记预测组合成数据帧;
• 从数据帧中删除预测值等于 0 的行;
• 计算度量并将其添加到 VotAver 结构中。
  

#---Metrics--train-------------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
      foreach(i = 1:4) %do% {# type threshold
        Ytest ->.; 
        ifelse(. == 0, -1, 1) ->.;
        cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% 
          as.data.frame() ->.; 
          dp$filter(., pred != 0) -> tbl 
        Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% 
          mean() %>% round(3)
        #Eval(tbl$actual,tbl$pred)
      } -> VotAver[[k]]$TrainScoreVot
    names(VotAver[[k]]$TrainScoreVot) <- type
    k <- k + 1
  }
}, env)
#---Metrics--test-------------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(i = 1:4) %do% {# type threshold
      Ytest1 ->.; 
      ifelse(. == 0, -1, 1) ->.;
      cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% 
        as.data.frame() ->.; 
      dp$filter(., pred != 0) -> tbl
      Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% 
        mean() %>% round(3)
      #Eval(tbl$actual,tbl$pred)
    } -> VotAver[[k]]$TestScoreVot
    names(VotAver[[k]]$TestScoreVot) <- type
    k <- k + 1
  }
}, env)
#---Metrics--test1-------------------------------------
evalq({
  k <- 1L #origin
  type <- qc(half, med, mce, both)
  while (k <= 4) { # group
    foreach(i = 1:4) %do% {# type threshold
      Ytest2 ->.; 
      ifelse(. == 0, -1, 1) ->.;
      cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% 
        as.data.frame() ->.; 
      dp$filter(., pred != 0) -> tbl 
      Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% 
        mean() %>% round(3)
      #Eval(tbl$actual,tbl$pred)
    } -> VotAver[[k]]$Test1ScoreVot
    names(VotAver[[k]]$Test1ScoreVot) <- type
    k <- k + 1
  }
}, env)

以可读的形式收集数据并查看它们:

#----TrainScoreVot-------------------
evalq({
  foreach(k = 1:4, .combine = "rbind") %do% {   # group
    VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
  } -> TrainScoreVot
  dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
           half   med   mce  both
origin    0.738 0.750 0.742 0.752
repaired  0.741 0.743 0.741 0.741
removed   0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
  foreach(k = 1:4, .combine = "rbind") %do% {   # group
    VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
  } -> TestScoreVot
  dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
           half   med   mce  both
origin    0.774 0.789 0.797 0.804
repaired  0.777 0.788 0.778 0.778
removed   0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
  foreach(k = 1:4, .combine = "rbind") %do% {   # group
    VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
  } -> Test1ScoreVot
  dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
           half   med   mce  both
origin    0.737 0.757 0.757 0.755
repaired  0.756 0.743 0.754 0.754
removed   0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713

最佳结果显示在 'removed' 数据组中的测试子集上，并处理了噪声样本。

再次，按照平均类型将每个数据组的每个子集中结果组合。

#==Variant-2==========================================
#--TrainScoreVotSum-------------------------------
evalq({
  k <- 1L
  while(k <= 4){ # group
    VotAver[[k]]$Train.clVoting ->.; 
    apply(., 1, function(x) sum(x)) ->.;
    ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum
    ifelse(Ytest == 0, -1, 1) ->.;
    cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; 
    as.data.frame(.) ->.; 
    dp$filter(., pred != 0) ->.; 
    Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; 
    mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum
    #Eval(tbl$actual,tbl$pred)
    k <- k + 1
  }
}, env)

#--TestScoreVotSum-------------------------------     
evalq({
  k <- 1L
  while(k <= 4){ # group                
    VotAver[[k]]$Test.clVoting ->.; 
    apply(., 1, function(x) sum(x))->.; 
    ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum
    ifelse(Ytest1 == 0, -1, 1) ->.;
    cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; 
    as.data.frame(.) ->.; 
    dp$filter(., pred != 0) ->.; 
    Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; 
    mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum
    #Eval(tbl$actual,tbl$pred)
    k <- k + 1
  }
}, env)

#--Test1ScoreVotSum-------------------------------  
evalq({
  k <- 1L
  while(k <= 4){ # group                
    VotAver[[k]]$Test1.clVoting ->.; 
    apply(., 1, function(x) sum(x))->.; 
    ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum
    ifelse(Ytest2 == 0, -1, 1) ->.;
    cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; 
    as.data.frame(.) ->.; 
    dp$filter(., pred != 0) ->.; 
    Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; 
    mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum
    #Eval(tbl$actual,tbl$pred)
    k <- k + 1
  }
}, env)

以可读的形式收集结果。

evalq({
  foreach(k = 1:4, .combine = "c") %do% {   # group
    VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
  } -> TrainScoreVotSum
  
  foreach(k = 1:4, .combine = "c") %do% {   # group
    VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
  } -> TestScoreVotSum
  
  foreach(k = 1:4, .combine = "c") %do% {   # group
    VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
  } -> Test1ScoreVotSum
  
  ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
  dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum, 
                                 Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
          TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin               0.763           0.807            0.762
repaired             0.752           0.802            0.748
removed              0.761           0.810            0.765
relabeled            0.766           0.825 (!!)       0.711  

考查测试集合的结果。 令人惊讶的是，relabeled 方法具有最好的结果。 所有组的结果都比 5.4 节中的结果好得多。 通过简单多数表决按级联将融合输出组合的方法令分类品质（Accuracy）从 5％ 提高到 7％。 

此部分的脚本位于 Voting_aver.R 文件中。 获得的数据结构如下图所示:

图例 10. VotAver 的数据结构。

下图提供了所有计算的简化方案：它展示出阶段，用到的脚本和数据结构。

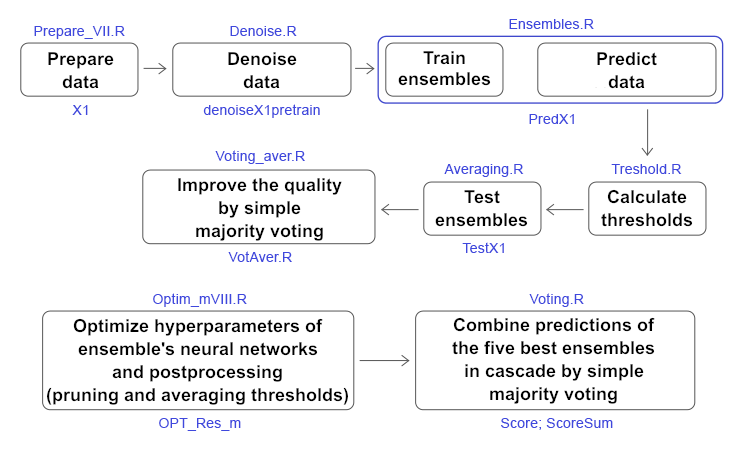
图例 11. 文章中主要计算的结构和顺序。

8. 分析实验结果

我们运用了三种方式处理 pretrain 子集 (!) 中初始数据集合里的噪声样本:

• 重新分配 "erroneously" 标记的数据，而无需更改类 (repaired) 的数量;
• 从子集 (removed) 中删除了 "noise" 样本;
• 将 "noise" 样本隔离在一个单独的类别中 (relabeled)。
  

已在 denoiseX1pretrain 结构中获取了四组数据 (origin, repaired, removed, relabeled)。 使用它们来训练由 500 个 ELM 神经网络分类器组成的融合。 获得四个融合。 使用这 4 个融合计算三个子集 Х1$train/test/test1 的连续预测，并将它们收集到 predX1 结构中。 

然后基于 InputTrain 子集 (!) 计算每个融合里 500 个神经网络中每一个的连续预测 4 种类型阈值。 使用这些阈值，将连续预测转换为类标签（0,1）。 计算融合的每个神经网络的度量 (mean(F1))，并在结构 testX1$$(InputTrainScore|InputTestScore|InputTest1Score) 中收集它们。 4 个数据组和 3 个子集中的度量分布可视化: 

• 首先，第一个测试子集的度量高于所有组中的 InputTrainS;
• 其次，repaired 和 removed 组中的度量在直观上高于其它两个。

现在选择每个融合中具有最大 mean(F1) 的 7 个最佳神经网络，并平均它们的连续预测。 将它们的值添加到结构中 testX1$$(TrainYpred|TestYpred|Test1Ypred)。 基于子集 TrainYpred 计算阈值 th_aver，确定所有平均连续预测的度量，并将它们添加到结构 testX1$$(TrainScore|TestScore|Test1Score) 中。 现在可以分析它们了。

不同数据组中修剪和平均阈值的不同组合，令我们获得了 0.75-0.77 范围内的度量。 在去除了 "noise" 样本的 removed 组中获得了最佳结果。 

优化神经网络的超参数可以在所有组中稳定地增加 0.77+ 的度量。    

优化神经网络的超参数和后期处理（修剪和平均）阈值，为所有已处理的 "noise" 样本数据组稳定地提供了约 0.78+ 的更佳结果。

使用最佳超参数从几个融合中创建一个超级融合，取这些融合的预测，并通过每个数据组的简单多数表决将它们组合在一起。 结果就是，得到 0.82+ 范围内 repaired 和 removed 组中的度量。 通过简单多数表决组合这些超级融合的预测，获得最终度量值 0.836。 所以，通过简单多数表决将预测级联组合起来可令品质提升 6-7％。 

在早期收到的融合的平均预测上验证此陈述。 在数据组中重复计算和转换后，在 Test 子集的 removed 组中收到 0.8+ 的度量。 继续以级联方式组合，在所有数据组的 Test 子集中接收值为 0.8+ 的度量。 

可以得出结论，通过简单投票表决将预测级联组合起来确实提高了分类品质。 

结束语

在本文中，我们研究了三种提高袋封融合品质的方法，以及优化融合神经网络和后期处理超参数。 根据实验结果，可得出以下结论：

• 使用 repaired 和 removed 方法处理噪声样本显著提高了融合的分类品质;
• 选择修剪和平均阈值类型，以及它们的组合显著影响分类品质;
• 将若干融合组合成一个超级融合，通过简单多数表决将它们的预测级联组合起来，令分类品质得到最大程度的提高;
• 优化融合神经网络的超参数和后期处理略微提高了分类品质得分。 建议对新数据执行初次优化，并在品质下降时定期重复。 周期性是通过实验确定的。

附件

GitHub/PartVIII 包括以下文件:

1. Importar.R — 导入函数包。
2. Library.R — 所需函数库。
3. FunPrepareData_VII.R — 准备初始数据得函数。
4. FunStacking_VIII.R — 创建并测试融合的函数。
5. Prepare_VIII.R — 为可训练组合器准备初始数据的函数和脚本。
6. Denoise.R — 用于处理噪声样本的脚本。
7. Ensemles.R — 创建融合的脚本。
8. Threshold.R — 确定阈值的脚本。
9. Test.R — 测试融合的脚本。
10. Averaging.R — 用于平均融合的连续输出的脚本。
11. Voting_aver.R — 通过简单多数表决将平均输出级联组合起来。
12. Optim_VIII.R — 用于优化神经网络超参数的脚本。
13. Optim_mVIII.R — 用于优化神经网络和后期处理超参数的脚本。
14. Voting.R — 通过简单多数表决将超级融合的输出级联组合起来。
15. SessionInfo_VII.txt — 文章中脚本用到的软件包列表。