在 1988 年，Constantino Tsallis 提出了 Boltzmann-Gibbs-Shannon 统计力学的泛化 [1]，其中，他提出了非广延熵的概念。
熵的泛化的一个重要推论似乎是新分布类型的存在 [2]，这些分布类型在新的统计力学中扮演着关键角色：
研究表明，这些分布类型可用于描述具有长期记忆的系统、长期作用力的系统以及强相关性系统内的大量经验数据。
熵与信息密切相关 [7]。参考文献 [8-9] 介绍了基于信息的统计力学泛化理论。经证明，新的非广延统计力学对经济也非常有用 [10-17]。例如，Q-Gaussian 分布充分描述了金融工具报价增量分布的宽翼（尾） (q~1.5)。据说，金融时间序列的大多数增量分布在较大的期间（月、年）上转换为正态分布 (q=1) [10]。
很自然地，期待统计力学的此类泛化会推出与 q-Gaussian 分布的中央极限定理类似的定理。但是参考文献 [18] 指出这是错的 —— 强相关随机变量之和的极限分布在分析上与 q-Gaussian 不同。
然而，另一个问题又出现了：研究表明，发现的精确解的数值非常接近 Q-Gaussian（“在数字上类似，在分析上不同”）。为了分析函数之间的差异并得出 Q-Gaussian 分布的最佳参数，在参考文献 [18] 中使用了一个级数展开。这些函数的关系导致表示系统非广延性程度的 q 参数的按幂展开。
应用统计的主要问题是接受统计假设的问题。长期以来它被视为一个无法解决的问题 [19-20]，需要特殊的工具（例如电子显微镜），使用现代应用统计方法，能够精准预测可能的走势。
参考文献 [21] 介绍的本征坐标法让我们能够达到更加深入的水平 —— 函数关系的结构化属性的分析。这个非常优秀的方法能用于解决各种各样的问题。参考文献 [22] 说明了与以上非广延分布相对应的函数的算子展开。
本文将介绍本征坐标法及其具体运用的例子。它包含很多公式，这些公式对理解方法的本质非常重要。在重复所有计算之后，您将能够为您感兴趣的函数描绘函数展开。
Q-Gaussian 分布在计量经济学中扮演着一个非常重要的角色 [4,10-17]。
为了一般性地理解当前研究水平，读者可以参考 Claudio Antonini 博士的著作《q-Gaussians in Finance》[23] （金融中的 q-Gaussian）和《The Use of the q-Gaussian Distribution in Finance》[24]（在金融中运用 q-Gaussian 分布）。
让我们简要说明一下主要的结果。
图 1. 科学法（幻灯片 4 “在金融中运用 q-Gaussian 分布”）
图 2 列出了金融时间序列的主要内容：
图 2. 金融时间序列的属性（幻灯片 3 “在金融中运用 q-Gaussian 分布”）
很多用于描述金融时间序列的理论模型得出 Q-Gaussian 分布：
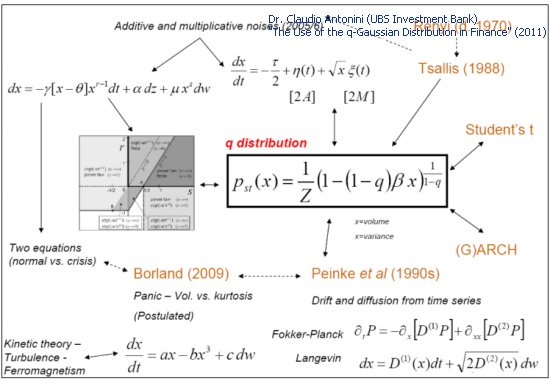
图 3. 理论模型和 Q-Gaussian（幻灯片 27 “在金融中运用 q-Gaussian分布”）
Q-Gaussian 分布也用于报价分布的现象性描述：
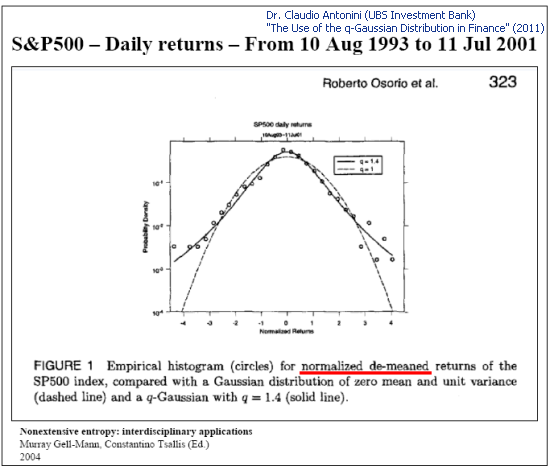
图 4. S&P 500 每日回报的抽样分析（幻灯片 8 “在金融中运用 q-Gaussian 分布”）
使用真实数据带来函数识别的问题：
图 5. 分布函数识别的问题（幻灯片 14 “金融中的 q-Gaussian”）
Claudio Antonini 博士的两篇论文都强调为了建立恰当的物理过程模型而正确识别函数的重要性：
图 6. “金融中的 q-Gaussian”和“在金融中运用 q-Gaussian 分布”得出的结论（Claudio Antonini 博士分别于 2010 年和 2011 年发表）
本征坐标展开如下所示：
其中 C1…CN 为常量，X1(t),..,XN(t) 为“本征坐标”。
此类线性展开非常方便，经常在数据分析中使用。例如，一个指数函数在对数刻度上转换为直线（可以使用线性回归轻松地计算其斜率）。因此，无需为了确定函数参数而进行非线性优化（拟合）。
然而，在处理更加复杂的函数（例如两个指数函数之和）时，对数刻度能提供的帮助极少 - 函数将不会作为一条直线出现。并且为了确定函数系数，需要进行非线性优化。
存在能够用几个函数解释经验数据一样棒的情形，所有这些函数对应于不同的物理过程模型。到底选择什么函数？哪个函数能够对经验数据反映的真实情况进行更充分的解释？
正确的函数识别对复杂系统（例如金融时间序列）的分析至关重要 - 每一种分布对应于某个物理过程，并且我们将能够更好地了解复杂系统的动态和一般属性，该系统具有选定的恰当模型。
应用统计 [19, 20] 表明，不存在用于拒绝错误统计假设的标准。本征坐标法抛出了有关这个问题（接受假设）的全新观点。
用于描述经验数据的函数可被视为某个微分方程的解。其形式确定本征坐标展开的结构。
本征坐标展开的一个特征是函数 Y(t) 生成的所有数据在函数 Y(t) 的本征坐标基 X1(t)..XN(t) 中在结构上是线性的。任何其它函数 F(t) 生成的数据在这个基中将不再作为一条直线出现（它们在函数 F(t) 的本征坐标基中将呈线性）。
此事实能够用于精确地识别函数，因此非常有利于统计假设的处理。
2.1. 本征坐标法
方法基于的概念是依据函数 Y(t) 以算子的形式建立本征坐标 Xk(t)。
可以使用数学分析来进行，其中本征坐标 Xk(t) 采用卷积积分的形式，通过函数 Y(t) 满足的微分方程的结构来确定展开。此外，还有确定系数 C1..CN 的问题。
在正交基展开中（例如在确定傅里叶变换系数时），通过将矢量投影到基来计算展开系数，并且由于基函数的正交性，得到需要的结果。
这并不适合我们的情况，因为没有与 X1(t)… XN(t) 的正交性有关的信息。
2.2. 使用最小二乘法计算展开系数
可以使用最小二乘法计算系数 Ck。此问题简化为解一个线性方程组。
假定：
对于 
的每一个度量，几乎都有一个误差 
：
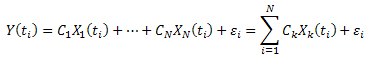
减去方差之和：
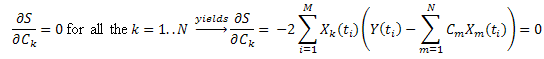
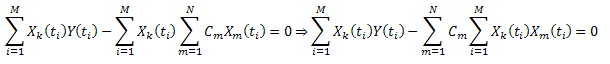
引入符号：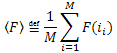
，它可表示为：
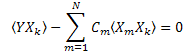
因此，我们得到一个 C1...CN (k=1..N) 的线性方程组：
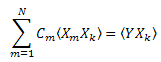
“相关性”矩阵是对称的： 
.
在某些情况下，本征坐标展开会以更加方便的积分形式出现：
它能减少误差的影响（因取平均所产生）但是需要额外的计算。
2.3. R(x) 函数展开示例
让我们看一看以下函数的本征坐标展开：
此函数生成几个统计分布 [21]：
-正态（高斯）分布；
-泊松分布；
- 伽玛分布；
- 
分布；
- Schtauffer 分布，包含 Weibull 分布作为一个特殊例子 
。此外，它还适用于描述驰豫过程：
- 普通指数函数；
- 广延指数函数；
- 幂驰豫函数。对 R(x) 按 x 进行微分，我们得到：
两边都乘以 x：
对 
进行变换：
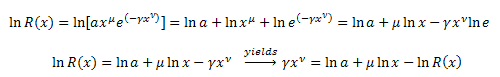
在等式中进行替代：
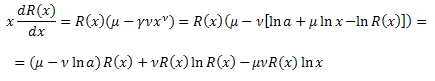
我们得到函数 R(x) 的微分方程：
在两边按 x 在区间 [xm,x] 进行积分：
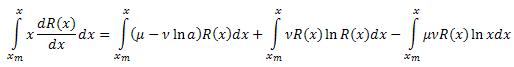
按以下部分对方程的左边进行积分：
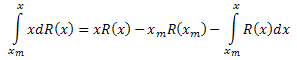
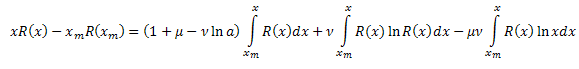
这样一来，我们得到：
其中：
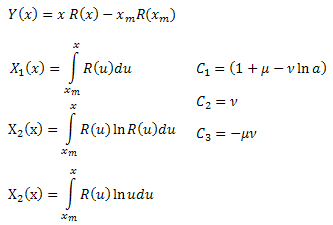
通过计算系数 
，我们能够确定函数参数 
。可以从 R(x) 的公式得到第四个参数 
。
2.4. 实施
展开系数的计算需要解线性方程组。为了便于处理矩阵，可以将其安排为单独的类 CMatrix（CMatrix.mqh 文件）。使用这个类的方法，可以设置矩阵参数、矩阵元素值并使用高斯方法解线性方程组。
//+------------------------------------------------------------------+ //| CMatrix class | //+------------------------------------------------------------------+ class CMatrix { double m_matrix[]; int m_rows; int m_columns; public: void SetSize(int nrows,int ncolumns); double Get(int i,int j); void Set(int i,int j,double val); void GaussSolve(double &v[]); void Test(); };
让我们提供一个脚本示例 (EC_Example1.mq5)，该示例计算函数 R(x) 的本征坐标和参数。
//+------------------------------------------------------------------+ //| EC_Example1.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <CMatrix.mqh> //+------------------------------------------------------------------+ //| CECCalculator | //+------------------------------------------------------------------+ class CECCalculator { protected: int m_size; //--- x[i] double m_x[]; //--- y[i] double m_y[]; //--- matrix CMatrix m_matrix; //--- Y[i] double m_ec_y[]; //--- eigen-coordinates X1[i],X2[i],X3[i] double m_ec_x1[]; double m_ec_x2[]; double m_ec_x3[]; //--- coefficients C1,C2,C3 double m_ec_coefs[]; //--- function f1=Y-C2*X2-C3*X3 double m_f1[]; //--- function f2=Y-C1*X1-C3*X3 double m_f2[]; //--- function f3=Y-C1*X1-C2*X2 double m_f3[]; private: //--- function for data generation double R(double x,double a,double mu,double gamma,double nu); //--- calculation of the integral double Integrate(double &x[],double &y[],int ind); //--- calculation of the function Y(x) void CalcY(double &y[]); //--- calculation of the function X1(x) void CalcX1(double &x1[]); //--- calculation of the function X2(x) void CalcX2(double &x2[]); //--- calculation of the function X3(x) void CalcX3(double &x3[]); //--- calculation of the correlator double Correlator(int ind1,int ind2); public: //--- method for generating the test function data set x[i],y[i] void GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu); //--- loading data from the file bool LoadData(string filename); //--- saving data into the file bool SaveData(string filename); //--- saving the calculation results void SaveResults(string filename); //--- calculation of the eigen-coordinates void CalcEigenCoordinates(); //--- calculation of the linear expansion coefficients void CalcEigenCoefficients(); //--- calculation of the function parameters void CalculateParameters(); //--- calculation of the functions f1,f2,f3 void CalculatePlotFunctions(); }; //+------------------------------------------------------------------+ //| Function R(x) | //+------------------------------------------------------------------+ double CECCalculator::R(double x,double a,double mu,double gamma,double nu) { return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x))))); } //+-----------------------------------------------------------------------+ //| Method for generating the data set x[i],y[i] of the test function R(x)| //+-----------------------------------------------------------------------+ void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu) { if(size<=0) return; if(x1>=x2) return; m_size=size; ArrayResize(m_x,m_size); ArrayResize(m_y,m_size); double delta=(x2-x1)/(m_size-1); //--- for(int i=0; i<m_size; i++) { m_x[i]=x1+i*delta; m_y[i]=R(m_x[i],a,mu,gamma,nu); } }; //+------------------------------------------------------------------+ //| Method for loading data from the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::LoadData(string filename) { int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } m_size=0; while(!FileIsEnding(filehandle)) { string str=FileReadString(filehandle); if(str!="") { string astr[]; StringSplit(str,';',astr); if(ArraySize(astr)==2) { ArrayResize(m_x,m_size+1); ArrayResize(m_y,m_size+1); m_x[m_size]=StringToDouble(astr[0]); m_y[m_size]=StringToDouble(astr[1]); m_size++; } else { m_size=0; return(false); } } } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for saving data into the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::SaveData(string filename) { if(m_size==0) return(false); if(ArraySize(m_x)!=ArraySize(m_y)) return(false); if(ArraySize(m_x)==0) return(false); int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } for(int i=0; i<ArraySize(m_x); i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for the calculation of the integral | //+------------------------------------------------------------------+ double CECCalculator::Integrate(double &x[],double &y[],int ind) { double sum=0; for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5; return(sum); } //+------------------------------------------------------------------+ //| Method for the calculation of the function Y(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; }; //+------------------------------------------------------------------+ //| Method for the calculation of the function X1(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X2(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i])); ArrayResize(x2,m_size); for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X3(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i])); ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the eigen-coordinates | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoordinates() { CalcY(m_ec_y); CalcX1(m_ec_x1); CalcX2(m_ec_x2); CalcX3(m_ec_x3); } //+------------------------------------------------------------------+ //| Method for the calculation of the correlator | //+------------------------------------------------------------------+ double CECCalculator::Correlator(int ind1,int ind2) { if(m_size==0) return(0); if(ind1<=0 || ind1>4) return(0); if(ind2<=0 || ind2>4) return(0); //--- double arr1[]; double arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); //--- switch(ind1) { case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break; } switch(ind2) { case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break; } //--- double sum=0; for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i]; } sum=sum/m_size; return(sum); }; //+------------------------------------------------------------------+ //| Method for the calculation of the linear expansion coefficients | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoefficients() { //--- setting the matrix size 3x4 m_matrix.SetSize(3,4); //--- calculation of the correlation matrix for(int i=3; i>=1; i--) { string s=""; for(int j=1; j<=4; j++) { double corr=Correlator(i,j); m_matrix.Set(i,j,corr); s=s+" "+DoubleToString(m_matrix.Get(i,j)); } Print(i," ",s); } //--- solving the system of the linear equations m_matrix.GaussSolve(m_ec_coefs); //--- displaying the solution - the obtained coefficients C1,..CN for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]); }; //+--------------------------------------------------------------------+ //| Method for the calculation of the function parameters a,mu,nu,gamma| //+--------------------------------------------------------------------+ void CECCalculator::CalculateParameters() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- calculate a double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1])); //--- calculate mu double mu=-m_ec_coefs[2]/m_ec_coefs[1]; //--- calculate nu double nu=m_ec_coefs[1]; //--- calculate gamma double arr1[],arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); double corr1=0; double corr2=0; for(int i=0; i<m_size; i++) { arr1[i]=MathPow(m_x[i],nu); arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]); corr1+=arr1[i]*arr2[i]; corr2+=arr1[i]*arr1[i]; } double gamma=-corr1/corr2; //--- Print("a=",a); Print("mu=",mu); Print("nu=",nu); Print("gamma=",gamma); }; //+------------------------------------------------------------------+ //| Method for the calculation of the functions | //| f1=Y-C2*X2-C3*X3 | //| f2=Y-C1*X1-C3*X3 | //| f3=Y-C1*X1-C2*X2 | //+------------------------------------------------------------------+ void CECCalculator::CalculatePlotFunctions() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- ArrayResize(m_f1,m_size); ArrayResize(m_f2,m_size); ArrayResize(m_f3,m_size); //--- for(int i=0; i<m_size; i++) { //--- plot function f1=Y-C2*X2-C3*X3 m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f2=Y-C1*X1-C3*X3 m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f3=Y-C1*X1-C2*X2 m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i]; } } //+------------------------------------------------------------------+ //| Method for saving the calculation results | //+------------------------------------------------------------------+ void CECCalculator::SaveResults(string filename) { if(m_size==0) return; int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename," for writing, error",GetLastError()); return; } for(int i=0; i<m_size; i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+=DoubleToString(m_ec_y[i],8)+";"; s+=DoubleToString(m_ec_x1[i],8)+";"; s+=DoubleToString(m_f1[i],8)+";"; s+=DoubleToString(m_ec_x2[i],8)+";"; s+=DoubleToString(m_f2[i],8)+";"; s+=DoubleToString(m_ec_x3[i],8)+";"; s+=DoubleToString(m_f3[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CECCalculator ec; //--- model function data preparation ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3); //--- saving into the file ec.SaveData("ex1.csv"); //--- calculation of the eigen-coordinates ec.CalcEigenCoordinates(); //--- calculation of the coefficients ec.CalcEigenCoefficients(); //--- calculation of the parameters ec.CalculateParameters(); //--- calculation of the functions f1,f2,f3 ec.CalculatePlotFunctions(); //--- saving the results into the file ec.SaveResults("ex1-results.csv"); }
2.5. R(x) 模型函数计算结果
我们将在区间 [0.25,15.25] 内生成函数 R(x) 的 100 个值作为模型数据
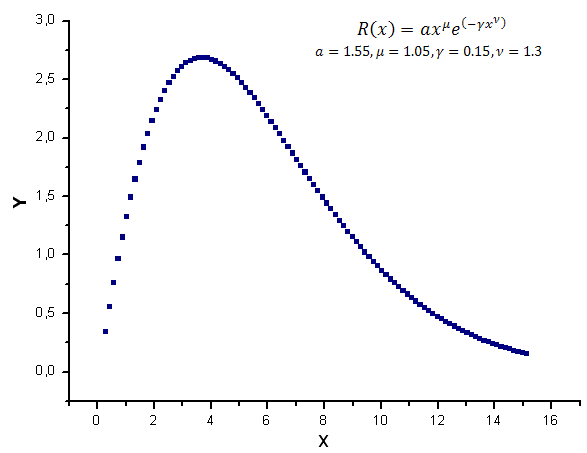
图 7. 用于计算的模型函数
这些数据为描绘函数 Y(x) 及其在函数 X1(x)、X2(x) 和 X3(x) 中的展开提供了基础。
图 8 显示函数 Y(x) 及其“本征坐标” X1(x)、X2(x) 和 X3(x)。
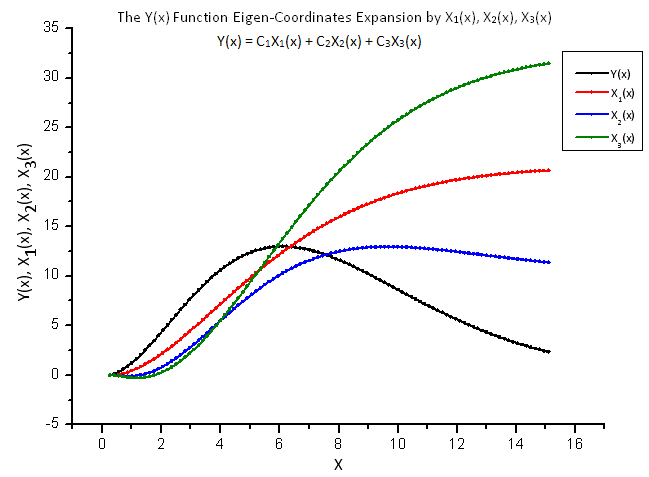
图 8. 函数 Y(x) 及其本征坐标 X1(x)、X2(x) 和 X3(x) 的一般形式
注意这些函数从算子 X1(x)、X2(x)和 X3(x) 的积分性质得出的平滑性。
在计算函数 Y(x)、X1(x)、X2(x) 和 X3(x) 之后，构建相关性矩阵，然后解系数 C1、C2 的 C3 的方程，并依据获得的值计算函数 R(x) 的参数：
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1 221.03637620 148.53278281 305.48547011 101.93843241 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2 148.53278281 101.63995012 202.85142688 74.19784681 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3 305.48547011 202.85142688 429.09345292 127.82779760
现在，我们检查计算出来的展开的线性。为此，我们需要计算 3 个函数。
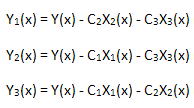
每个函数投影在其本征坐标基 X1(x)、X2(x) 和 X3(x) 上：
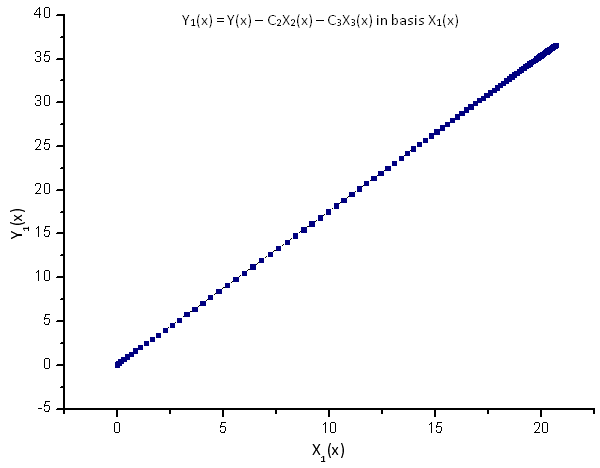
图 9. 函数 Y1(x) 在基 X1(x) 上的表示
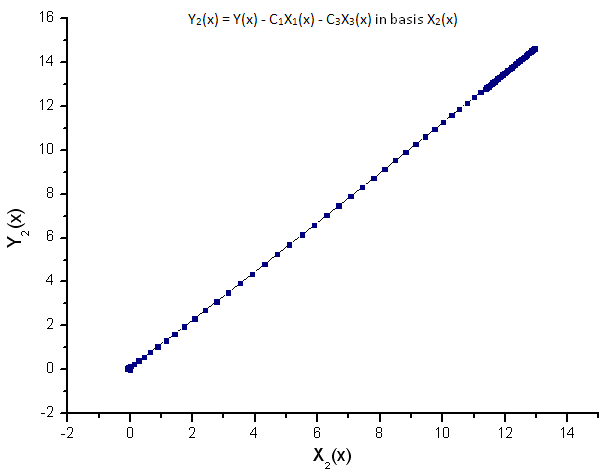
图 10. 函数 Y2(x) 在基 X2(x) 上的表示
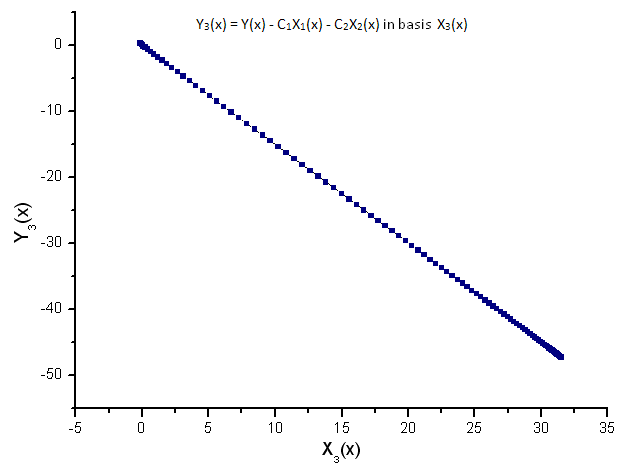
图 11. 函数 Y3(x) 在基 X3(x) 上的表示
描绘出来的函数的线性依存关系表明图 7 中的数据序列与函数 R(x) 严格相关。
以 R(x) 本征坐标表示的任何其他函数（甚至在形式上类似）将不再具有线性形式。此事实让我们能够识别函数。
如果点的数量增加到 10000（同时保持相同的区间），则可以提高计算模型函数参数的数值的准确性：
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1 225.47846911 151.22066473 311.86134419 104.65062550 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2 151.22066473 103.30005101 206.66297964 76.03285182 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3 311.86134419 206.66297964 438.35625824 131.91955339
在本例中，已经更加准确地计算了函数参数。
2.6 噪声效应
实际的经验数据始终包含噪声。
在 ECCCalculator 类的 GenerateData() 方法中，我们将：
m_y[i]=R(m_x[i],a,mu,gamma,nu);
替换为
m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;
添加了一个随机噪声，大概是最大函数值的 10%。
EC_Example1-noise.mq5 脚本的结果如下所示：
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1 254.45082565 185.19087989 354.25574000 125.17343164 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2 185.19087989 136.81028987 254.92996885 97.14705491 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3 354.25574000 254.92996885 501.76021715 159.49440494
图 12 显示具有随机噪声的模型函数图。
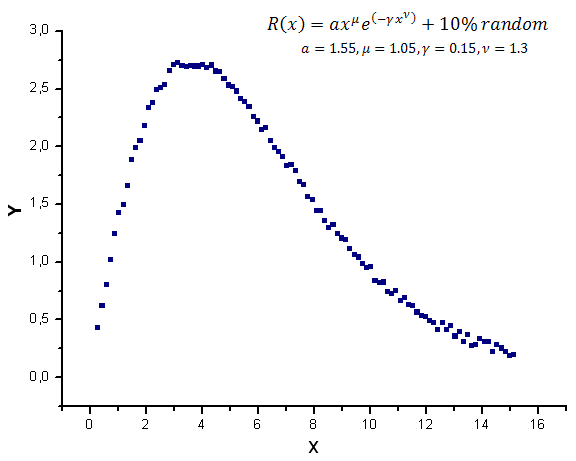
图 12. 用于计算的具有噪声的模型函数
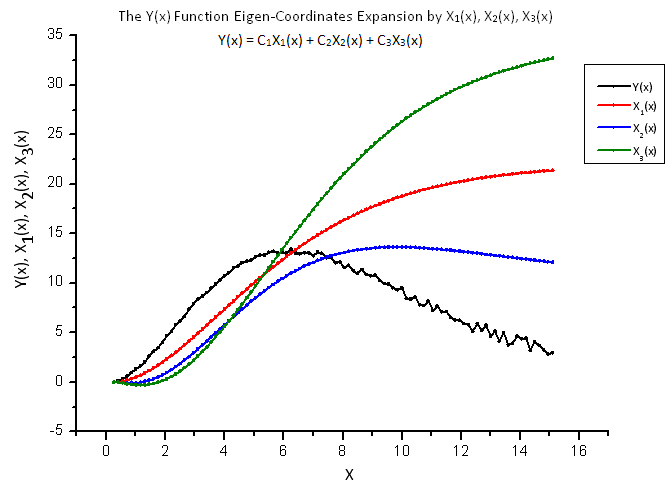
图 13. 函数 Y(x) 及其本征坐标 X1(x)、X2(x) 和 X3(x) 的一般形式
用作“本征坐标”的函数 X1(x)、X2(x) 和 X3(x) 看起来仍然是平滑的，然而描绘为它们的线性组合的 Y(x) 看起来有所不同（图 13）。
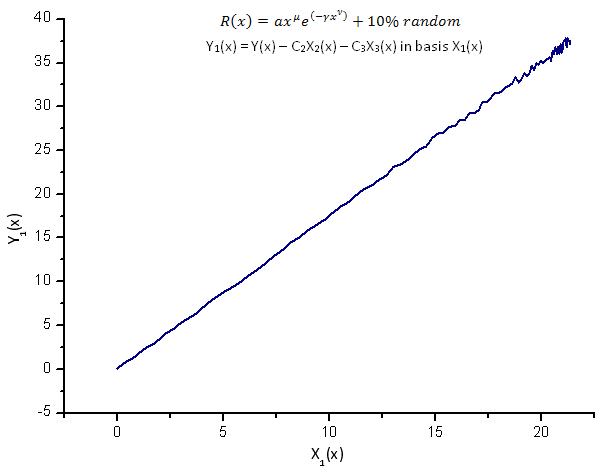
图 14. 函数 Y1(x) 在基 X1(x) 上的表示
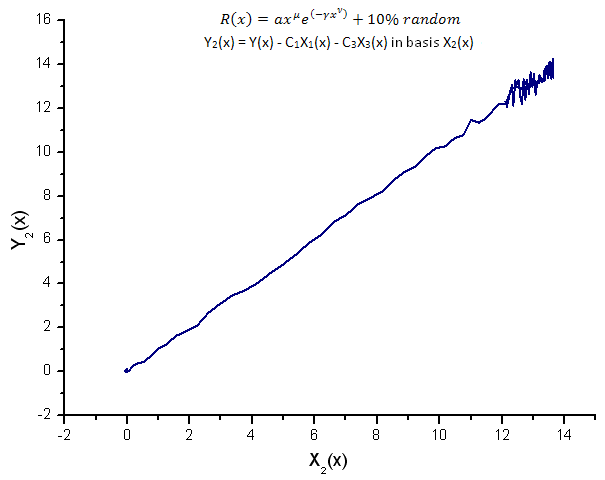
图 15. 函数 Y2(x) 在基 X2(x) 上的表示
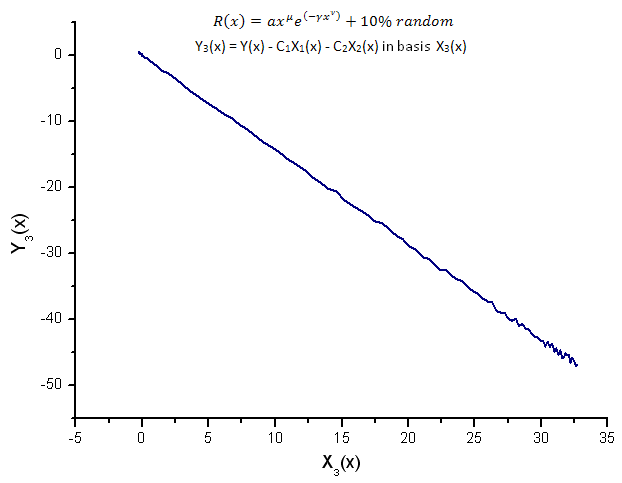
图 16. 函数 Y3(x) 在基 X3(x) 上的表示
函数 Y1(x)、Y2(x) 和 Y3(x) 在本征坐标基上的表示（图 8-10）仍然具有线性形式，尽管读者可以注意到由于噪声的存在，围绕直线有一定的波动。至于较大的 X，其中信号/噪声比变得较小，这种情况更为明显。
在这里，噪声分量位于直线的两端，因而在本例中，使用积分本征坐标展开非常方便（第 2.2 节）。
统计力学的泛化导致各种分布 [2, 22]：
其中 
，
。
q-Gaussian 分布是函数 P2(x) 的特殊情形。
3.1. P1(x) 函数本征坐标展开
我们对 P1(x) 进行微分：
生成的微分方程如下所示：
在区间 [xm,x] 上进行积分：
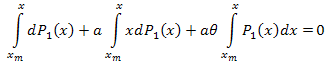
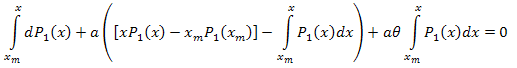
因此：
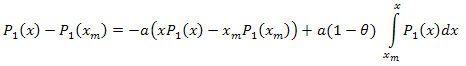
本征坐标展开如下所示：
其中：
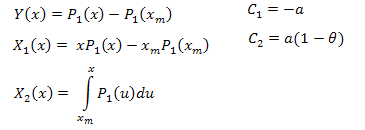
用于计算的函数如下所示 (EC_Example2.mq5)：
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); //--- Y=P(x)-P(xm) for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=x*P(x)-xm*P(xm) for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=Integrate(P1(x)) for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i); }
此时相关性矩阵大小为 2x3；函数 P1(x) 的参数 a 和 θ 的值依据系数 С1 和 C2 来确定。参数 B 的数值可从正态化要求来获得。
以下是模型函数 P1(x,1,0.5,2) 在区间 x [0,10] 内的计算结果；使用的点数为 1000：
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1 0.15420524 0.48808959 -0.32145543 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2 0.48808959 1.79668322 -1.14307410图 17-20 显示了函数 P1(x) 及其本征坐标展开。
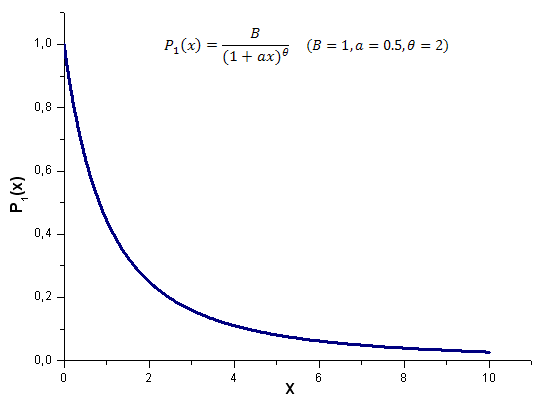
图 17. 用于计算的模型函数 P1(x, 1, 0.5, 2)，1000 点
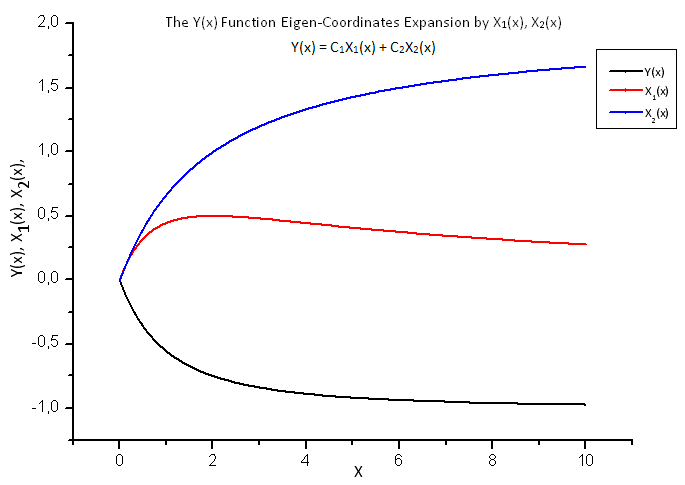
图 18. 函数 Y(x) 及其本征坐标 X1(x) 和 X2(x) 的一般形式
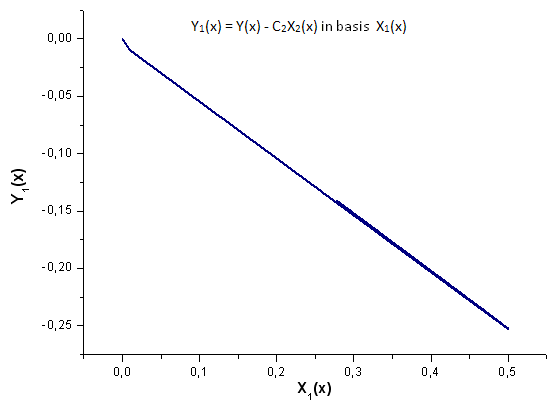
图 19. 函数 Y1(x) 在基 X1(x) 上的表示
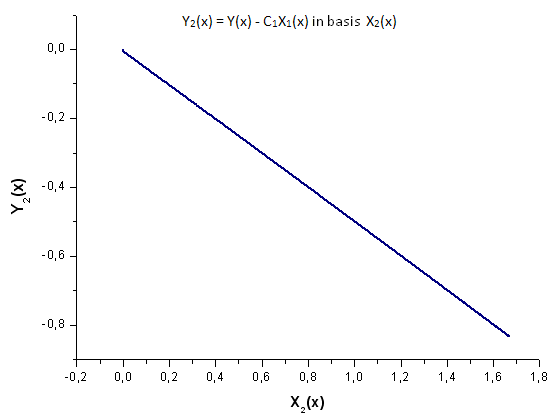
图 20. 函数 Y2(x) 在基 X2(x) 上的表示
请仔细观察图 19。线性依存关系在图的开头和三分之二处有稍微的变形。这与所计算展开的特性有关 - X1(x) 不是积分性质。
3.2. P2(x) 函数本征坐标展开
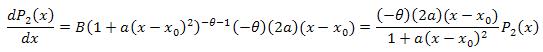
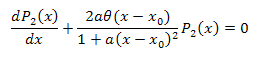
微分方程：
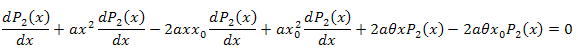
我们在两边按 x 在区间 [xm,x] 进行积分：
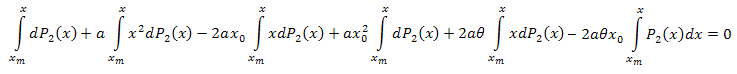
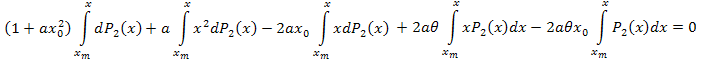
按部分进行积分，我们得到：
进行简化：
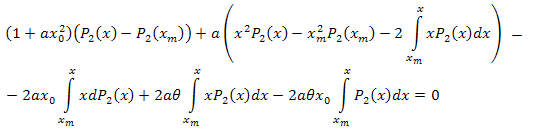
经过代数处理之后，我们得到：
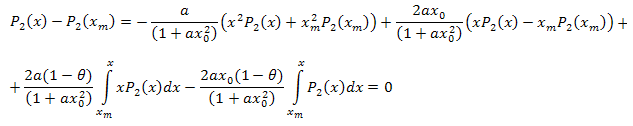
因此，生成的展开如下所示：
其中：
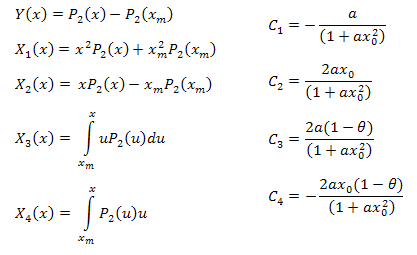
可以使用下面的公式计算函数参数：
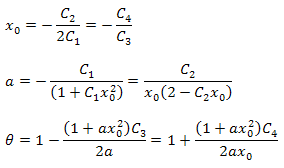
应该指出，生成的展开中各参数之间有其他关系。此事实可用于证明为分析选择的函数是否正确。对于与函数 P2(x) 严格对应的数据，这些关系始终是成立的。
参数 B 的数值可从正态化要求来获得。
用于计算本征坐标的函数如下所示 (EC_Example3.mq5)：
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm) for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=(x)*P2(x)-(xm)*P2(xm) for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX3 | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i]; //--- X3=Integrate(X*P2(x)) ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| CalcX4 | //+------------------------------------------------------------------+ void CECCalculator::CalcX4(double &x4[]) { if(m_size==0) return; //--- X4=Integrate(P2(x)) ArrayResize(x4,m_size); for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i); }
以下是模型函数 P2(x) 的计算结果（B=1，a=0.5， θ=2，x0=1）；使用的点数为 1000：
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1 1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2 0.60684314 0.37995888 0.55974145 0.58899739 0.06731011 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3 1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4 1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168图 21-26显示了函数 P2(x) 及其本征坐标展开。
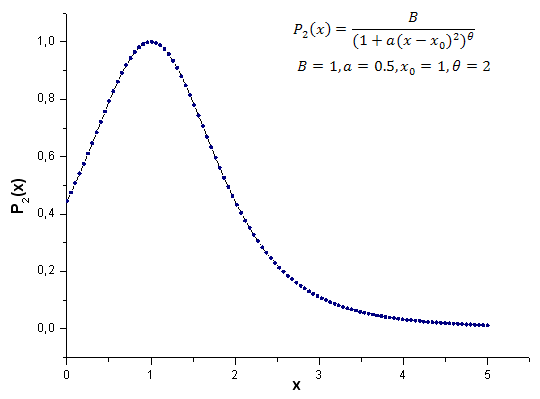
图 21. 用于计算的模型函数 P2(x,1,0.5,2,1)，100 点
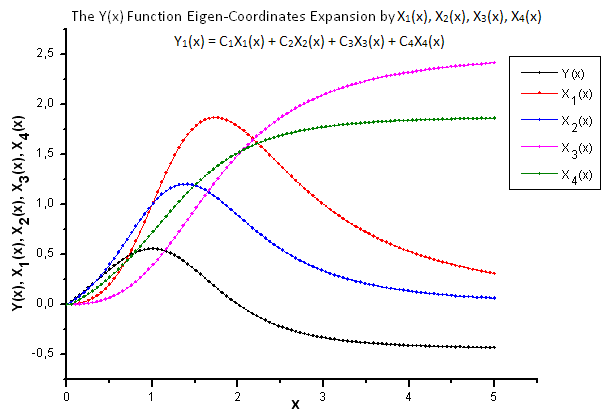
图 22. 函数 Y(x) 及其本征坐标 X1(x)、X2(x)、 X3(x) 和 X4(x) 的一般形式
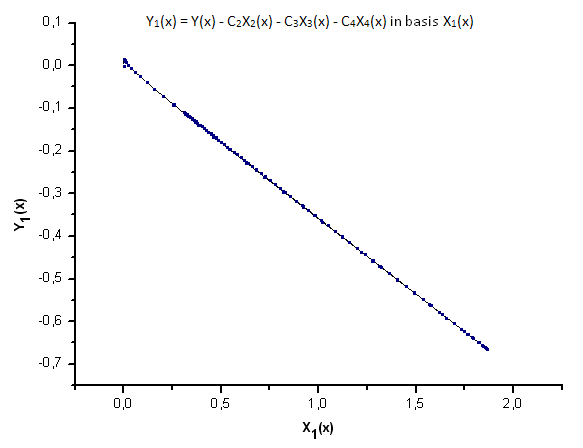
图 23. 函数 Y1(x) 在基 X1(x) 上的表示
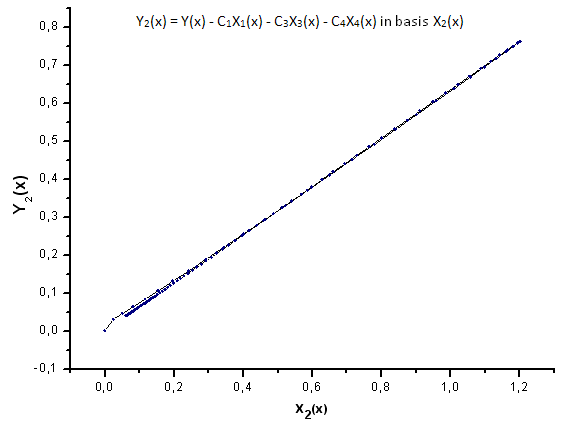
图 24. 函数 Y2(x) 在基 X2(x) 上的表示
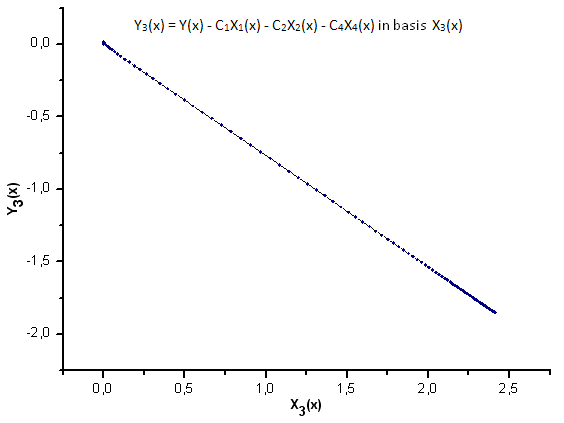
图 25. 函数 Y3(x) 在基 X3(x) 上的表示
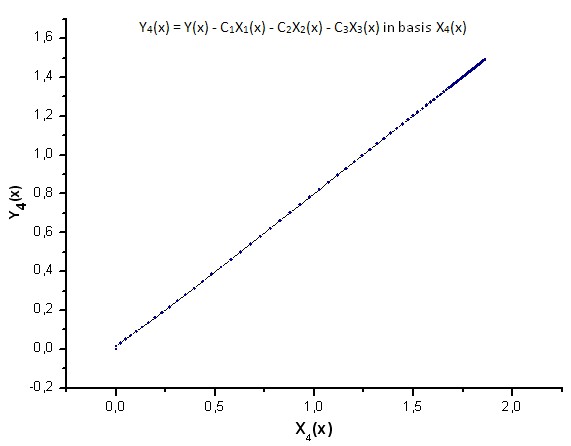
图 26. 函数 Y4(x) 在基 X4(x) 上的表示
q-Gaussian 分布家族处于非广延统计力学的非常中心的地位，因此很自然地期待它会在泛化中央极限理论中出现。熵考虑因素是支持它的主要论据 [26]。
然而，参考文献 [18, 演示文稿] 表明 q-Gaussian 等分布不是通用的，因此对它们作为极限分布的特殊角色感到怀疑。
例如，使用 q-Gaussian 分布，函数（其中一个问题的分析解）：
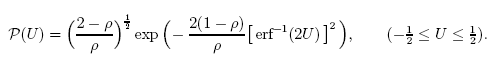
能被非常精确地描述。
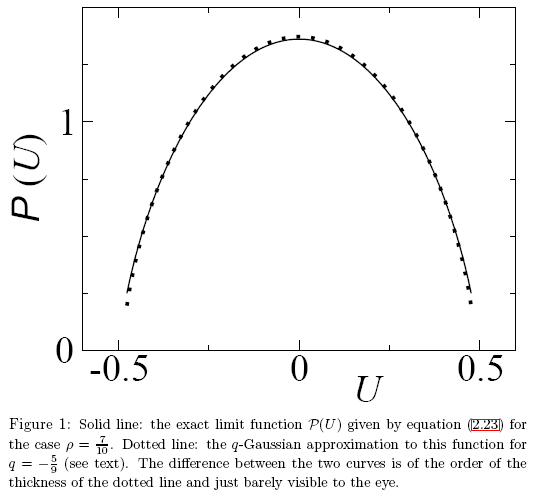
图 27. 论文《关于统计力学中 q-Gaussian 和非高斯分布的说明》中的一个例子
在这个例子中，在分析上，微分函数具有类似的数值，因此肉眼很难看到差异。需要精确的函数识别方法。可以使用本征坐标法很好的解决这个问题。
让我们回顾一下 P(U) 函数本征坐标展开的例子，并说明到底是什么让它与 q-Gaussian 不同。这些函数看起来非常相似（图 27）。
我们生成一个信号（P(U) 函数的 100 个值），并将其“投影”到在第 3.2 节中描绘的 P2(x) 函数本征坐标系上。
Hilhorst-Schehr-problem.mq5 脚本计算 P(U) 函数并构建要保存在 MQL5\Files\test-data.csv 文件中的数据序列。用 EC_Example3_Test.mq5 分析这些数据。
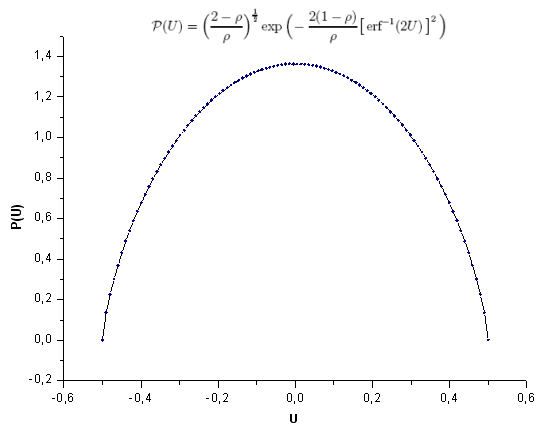
图 28. 模型函数 P(U)，100 点
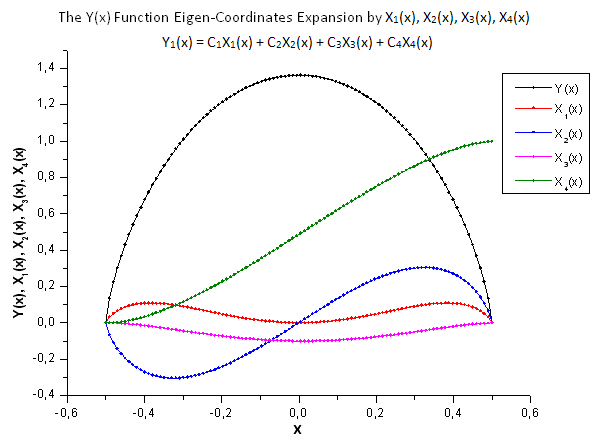
图 29. 函数 Y(x) 及其本征坐标 X1(x)、X2(x)、 X3(x) 和 X4(x) 的一般形式
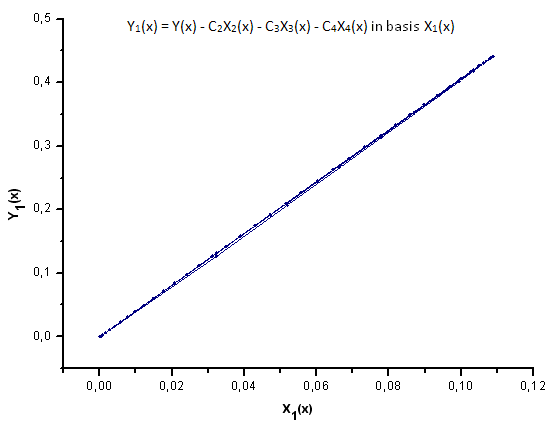
图 30. 函数 Y1(x) 在基 X1(x) 上的表示
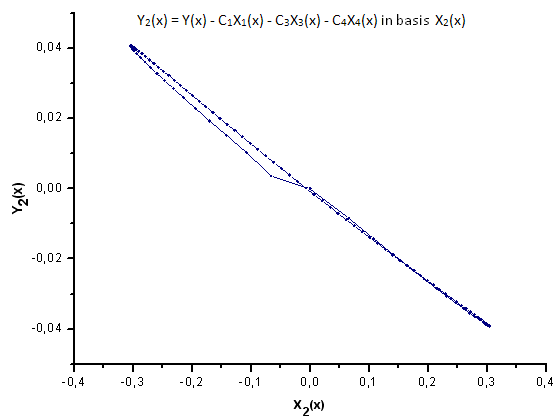
图 31. 函数 Y2(x) 在基 X2(x) 上的表示
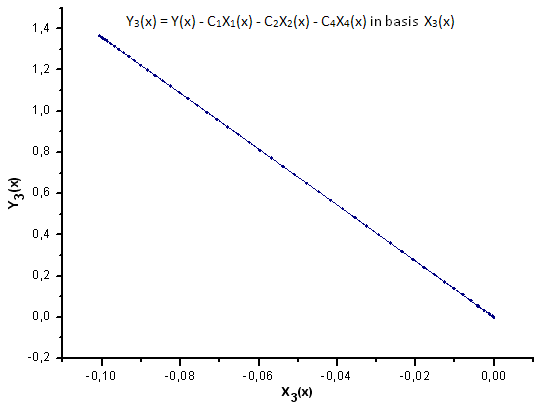
图 32. 函数 Y3(x) 在基 X3(x) 上的表示
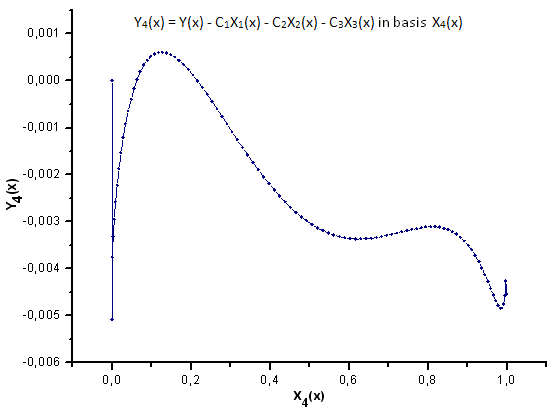
图 33. 函数 Y4(x) 在基 X4(x) 上的表示
如图 30-33 所示，函数 P2(x) 和 P(U) 在坐标 X1(x)、X2(x) 和 X3(x) 上非常类似 —— 读者可以在 Xi(x) 和 Yi(x) 之间看到非常好的线性依存关系。可以在分量 X4(x) 中看到一个显著的差异（图 33）。
分量 X4(x) 缺少线性依存关系证明 P(U) 生成的数据集，尽管在外观上与 q-Gaussian 分布类似，但实际上不是 q-Gaussian。
我们可以通过将 Xi(x) 和 Yi(x) 标绘在一起，以不同的方式来查看函数（图 34-37）。
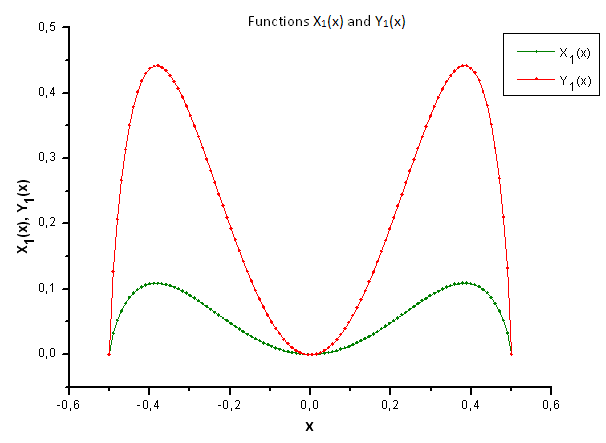
图 34. 函数 X1(x) 和 Y1(x) 的一般形式
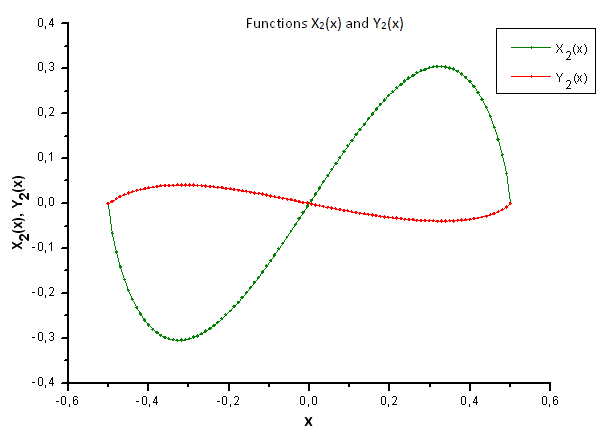
图 35. 函数 X2(x) 和 Y2(x) 的一般形式
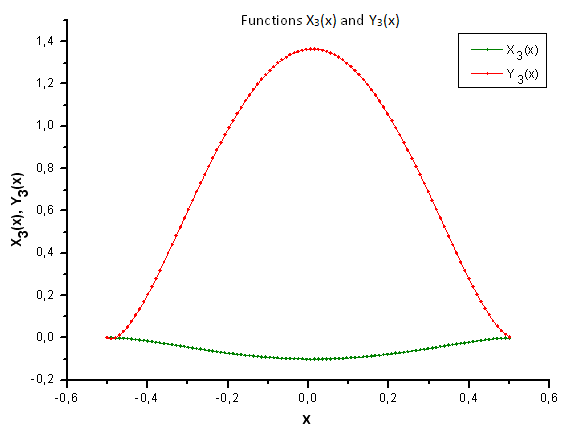
图 36. 函数 X3(x) 和 Y3(x) 的一般形式
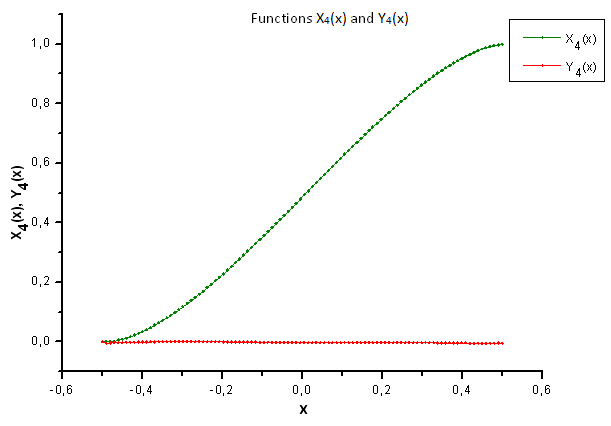
图 37. 函数 X4(x) 和 Y4(x) 的一般形式
如图 37 所示，分量 X4(x) 中的结构差异在将函数 P(U) 生成的数据投影到函数 P2(x) 的本征坐标上时变得很明显。因此，我们可以肯定地说经验数据不对应函数 P2(x)。
以下列出的计算 (EC_Example3_test) 也支持这一事实：
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1 0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2 0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3 -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4 0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994
它还削弱了参数之间的关系。
本征坐标法是一款用于分析函数关系的结构化属性的独特工具，能够实质性简化对数据的分析和解释。
此方法基于的概念是使用经验数据集 {xi,yi} 构建与所提议的模型相对应的新函数。算子展开的形式由函数满足的微分方程的结构来决定，而函数是数据描述的“候选者”。如果函数是固有函数，则使用数据 {xi,yi} 计算的函数展开在本征坐标基中将呈现线性。“候选函数”的本征坐标基中的线性偏离表明给定函数不能生成数据 {xi,yi}，并且构建的模型不恰当。
在某些复杂的情形中，候选函数和固有函数可能看起来非常类似，计算出来的大部分展开呈线性。尽管如此，本征坐标法让我们能够识别这些函数之间的差异，我们可以通过展开的线性被削弱来知道其存在 - Hilhorst 和 Schehr 的例子说明投影到 X4(x) 上时，最后的展开成员中的差异变得非常明显。
在处理函数 P2(x) 满足的微分方程（第 3.2 节）时，此信息也非常有用 —— 就 P2(x) 而言，所讨论的成员与对应于线性部分。如果对经验数据进行现象性描述，则可能不是如此有趣（“我们正在寻找以 q-Gaussian 形式出现的解”）。然而，如果模型以微分方程（图 3）为基础，则能够更好地理解在物理过程模型中考虑的各个机制的角色。
本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
