本系列的前一篇文章 讨论了 DNN 模型的超参数,并用若干示例对其进行了训练,且对其进行了测试。 所得模型的品质非常高。
我们还讨论了如何提高分类品质的可能性。 其中之一是使用神经网络的融合。 这个增幅的变体将在本文中讨论。
研究表明,分类器融合通常比单体分类器更准确。 这样的一个融合如图例 1a 所示。 它使用了若干个分类器,每个分类器都针对输入的对象进行决策。 然后,这些独立决策在合并器中聚合。 融合输出对象的类标签。
直观上,分类器融合不能被严格定义。 这般不确定性如图例 1b-d 所示。 本质上,任何融合本身都是一个分类器 (图例 1b)。 包含它的基本分类器将提取 (通常是隐式的) 规则性的复杂函数,并且合并器将成为这些函数的简单分类器聚合。
另一方面,没有什么能阻止我们将传统的标准神经网络分类器称为融合 (图例 1c)。 倒数第二层上的神经元可被认为是单独的分类器。 它们的决策必须在合并器中 "解密",合并器的角色由顶层扮演。
最终,函数可被视为原始分类器,而分类器可被视为它们的复杂合并器 (图例 1d)。
我们结合简单的可训练分类器来获得准确的分类决策。 但这是前进的正确道路吗?
Tin Kam Ho 在 2002 年出版的论文 "多个分类器合并: 课题与后续步骤" 中写道:
"现在我们寻找最佳的分类器集合,然后寻找最佳的合并方法,来替代寻找最佳的特征集合与最佳的分类器。 可以想象,我们很快就会寻找到最好的合并方法,然后是使用它们的最好方法。 如果我们不抓住机会回顾这一挑战所引发的根本问题,我们必然会陷入这种无休止的往复,拖着越来越复杂的合并方案和理论,逐渐忽视原有的问题。"
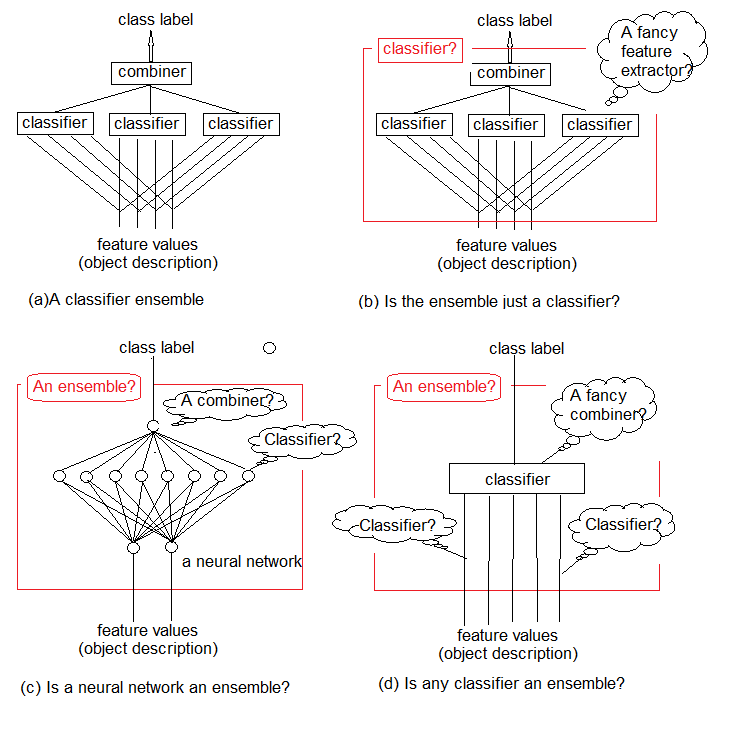
图例 1. 什么是分类器的融合?
这一课题就是我们必须在创建新的复杂项目之前找到使用现有工具和方法的最佳方式。
众所周知,神经网络的分类器是 "泛逼近"。 这意味着任何分类边界,无论其复杂度如何,都可以通过具有任何所需精度的有限神经网络来逼近。 不过,这些知识并没有为我们提供创建或训练这种网络的方法。 合并分类器的思路是尝试通过组成托管网络建筑区块来解决问题。
组成融合的方法是元算法,它将若干机器学习方法合并成一个预测模型,以便:
这些方法可划分为两组:
大多数融合方法在创建同质基础模型时使用单一基础学习算法。 这导致了同质融合。 还有使用异构模型的方法 (不同类型的模型)。 结果就是,形成了异质融合。 为了令融合比任意单体成员更准确,基础模型应尽可能多元化。 换言之,来自基础分类器的信息越多,融合的准确性就越高。
图例 2 示意了创建一个分类器融合的 4 个级别。 问题会出现在它们当中的每一个上,下面将对它们进行讨论。

图例 2. 创建分类器融合的四个级别
我们来更详尽地讨论这个问题。
有些融合方法没有定义合并器。 但对于这样做的方法,有三种类型的合并器。
基础分类器的训练应并行 (独立) 还是顺序? 顺序训练的一个示例是 AdaBoost,其中每个添加的分类器的训练集合取决于在它之前创建的融合。
如何在融合中产生差异? 建议使用以下选项。
如何确定融合中的分类器数量? 融合能否由同时训练所需数量的分类器或通过添加/删除分类器迭代构建? 可能的选项:
一些融合方法可与任何分类器模型一起使用,而其它方法则与某种类型的分类器相关联。 "分类器特定" 融合的示例是一个随机森林。 它的基础分类器是决策树。 因此,有两种方法变体:
在训练和优化分类器融合的参数时,应区分解决方案优化和覆盖优化。
融合分解旨在降低问题的复杂性,因此它似乎是合理的。
在著作 组合形态分类器。 方法和算法,第二版。 Ludmila Kuncheva 和 融合方法。 基础和算法 中详尽分析并深入研究了融合的方法。 建议阅读它们。
该方法的名称衍生自短语 Bootstrap AGGregatING (引导聚合)。 引导聚合融合创建如下:
我们回到图例 2 并分析应用引导聚合方法来创建一个分类器融合的所有级别。
在该级别,从分类器获得的数据被合并,且聚合成单一输出。
我们如何合并单体输出? 使用一个不可训练的合并器 (平均,简单多数表决)。
在级别 B,所有使用分类器的工作都会发生。 这里出现了若干问题。
我们来更详细地阐述这一点。 分类器选择及其论证是工作中的重要部分。 我们列出基础分类器的主要需求,以便创建高质量的融合。
首先,分类器必须简单: 不建议使用深度神经网络。
其次,分类器必须是不同的: 具有不同的初始化,学习参数,训练集合,等等。
第三,分类器速度很重要: 模型不应花费数小时来训练。
第四,分类模型应较弱,预测结果略好于 50%。
最后,分类器的不稳定性很重要,因此预测结果的范围很广。
有一个选项可以满足所有这些需求。 它是一种特殊类型的神经网络 — ELM (极端学习机器), 它被提议作为备选学习算法来替代 MLP。 形式上,它是有一个隐藏层的完全连接的神经网络。 但是,如果没有迭代权重确定 (训练),它变得异常快速。 它在初始化期间随机选择隐藏层中神经元的权重,然后根据所选择的激活函数分析确定它们的输出权重。 有关 ELM 算法的详细说明及其多种类型的概述,请参见附带的存档。
在此级别,源数据被馈送到神经网络的输入以便进行训练。
如何操纵输入数据以便提供高度多样性和高度个性化的精度?引导样本将单独用于每个分类器。 引导样本的大小对于所有集合成员都是相同的,但它将会被优化。
为了用 ELM 集合进行实验,R 语言中有两个软件包 (elmNN, ELMR),在 Python 中有一个 (hpelm)。 现在,我们来测试 elmNN 软件包的功能,它实现了经典的 ELM。 elmNN 软件包设计用于利用 ELM 的批处理方法进行创建、训练和测试。 因此,训练和测试样本在训练之前准备好,并一次性馈送入模型。 软件包很简单。
该实验将包括以下阶段。
实验中使用最新版本的 MRO 3.4.3。 它实现了几个适合我们工作的新软件包。
运行 RStudio, 进入 GitHub/Part_I 下载取自终端的报价文件 Cotir.RData, 并从 GitHub/Part_IV 中提取含有数据准备函数的 FunPrepareData.R 文件。
之前,已确定一套带有推算异常值和常规化数据的数据,可以在预训练中获得更好的结果。 我们会用到它。 您还可以测试之前考虑的其它预处理选项。
当划分为 pretrain/train/val/test 子集时,我们使用第一次机会来提高分类品质 — 增加训练样本数量。 'pretrain' 子集中的样本数量将增加到 4000。
#----准备------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---准备---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
通过更改 SplitData() 函数中的 start 参数,可以获得向右顺移 'start' 量的集合。 这可在将来检查价格范围不同部分的品质,并判断其在历史中是如何变化的。
创建用于训练和测试的数据集合 (pretrain/train/test/ test1),收集在 X 列表中。 将目标从分数转换为数字类型 (0.1)。
#---数据 X-------------
evalq({
list(
pretrain = list(
x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1)
),
train = list(
x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1)
),
test = list(
x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1)
),
test1 = list(
x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1)
)
) -> X
}, env)
测试函数 clusterSim::HINoV.Mod() (参阅软件包获取详细信息)。 它基于具有不同距离和方法的集群对变量进行排序。 我们将使用默认参数。 您可以自由地尝试使用其它参数。 常数 numFeature <- 10 允许改变馈送到模型的最佳预测器 bestF 的数量。
计算依据 X$pretrain 集合执行
require(clusterSim)
evalq({
numFeature <- 10
HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> r
r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
[,1] [,2]
[1,] 5 0.9242887
[2,] 11 0.8775318
[3,] 9 0.8265240
[4,] 3 0.6093157
[5,] 6 0.6004115
[6,] 10 0.5730556
[7,] 1 0.5722479
[8,] 7 0.4730875
[9,] 4 0.3780357
[10,] 8 0.3181561
[11,] 2 0.2960231
[12,] 12 0.1009184
排序预测器的顺序显示在上面的代码清单中。 前 10 名列在下面,在未来会用到它们。
> colnames(env$X$pretrain$x)[env$bestF] [1] "v.fatl" "v.rbci" "v.ftlm" "rbci" "v.satl" "v.stlm" "ftlm" [8] "v.rftl" "pcci" "v.rstl"
实验集合已经准备就绪。
用于从测试结果计算度量衡的 Evaluate() 函数取自本系列的 上一篇文章。 mean(F1) 的数值将用作优化 (最大化) 标准。 将此函数加载到 'env' 环境中。
训练神经网络的融合 (n < - 500 个单位),将它们合并在 Ens 中。 每个神经网络都依据自己的样本进行训练。 通过随机替换训练集合中提取的 7/10 个例子来生成样本。 必须为模型设置两个参数: 'nh' — 隐藏层中的神经元数量和 'act' — 激活函数。 该软件包为激活函数提供以下选项:
考虑到有 10 个输入变量,我们首先取 nh = 5。 激活函数取 actfun = "sin"。 融合学得很快。 我根据神经网络的经验直觉地选择了参数。 您可以尝试其它选项。
#---3-----Train---------------------------- evalq({ n <- 500 r <- 7 nh <- 5 Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } }, env)
我们简要地研究脚本中的计算。 定义常数 n (融合中神经网络的数量) 和 r (用于训练神经网络的引导样本的大小)。 对于融合中的每个神经网络,样本将会不同。 nh 是隐藏层中的神经元数量。 然后使用主集合 X$pretrain 定义输入数据集合 Xtrain,并仅保留某些预测器 bestF。
这产生了由 500 个单体神经网络分类器组成的融合 Ens[[500]]。 测试基于从主集合 X$train 中利用最佳预测器 bestF 获得的测试集合 Xtest 上进行。 生成的结果是 y.pr[1001,500] - 500 个连续预测变量的数据帧。
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env)
融合的基础分类器可以具有以下输出类型:
基础分类器在输出处具有连续的数值变量 (支持度)。 输入 X 的支持度能以不同方式解释。 它可以是提议标签的可靠性,或评估类的可能概率。 对于我们的情况,提议的分类标签的可靠性将作为输出。
第一种合并方式是 平均: 获取单体输出的平均值。 然后将其转换为类标签,而 转换阈值 取为 0.5。
合并的第二种变体是简单的 多数表决。 为此,每个输出首先从连续变量转换为类标签 [-1,1] (转换阈值为 0.5)。 然后将所有输出累加,如果结果大于 0,则分配类 1,否则分配类 0。
使用获得的类标签,确定度量衡 (准确率, 精确率, 召回率 和 F1)。
基础分类器的数量最初是富余的,以便稍后从中选择最好的。 执行此操作时应用以下方法:
融合修剪与预测器的选择相同。 所以,在选择预测器时,可以应用相同的方法 (这已在本系列的前几篇文章中介绍过)。
按分类误差 (降低误差修剪) 排序的融合当中进行选择,将之用于进一步的计算。
总之,在实验中将使用以下方法:
将单体输出从连续变量转换为类标签的阈值是 0.5。 预先警告: 这不是最好的选择,而是最简单的选择。 它可以在以后改进。
a) 确定融合的最佳单体分类器
确定所有 500 个神经网络的 mean(F1),选择若干具有最佳得分的 "bestNN"。 多数表决的最佳神经网络的数量必须是奇数,因此它将被定义为: (numEns*2 + 1)。
#---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
我们简要地研究脚本中的计算。 在 foreach() 循环中,将每个神经网络的连续预测 y.pr[ ,i] 转换为数值 [0,1],确定该预测得 mean(F1),并输出该值作为向量 Score[500]。 然后按降序对向量 Score 的数据进行排序,确定具有最佳 (最高) 得分的 bestNN 神经网络的索引。 输出 Score[bestNN] 的这些最佳成员的度量衡数值,四舍五入到小数点后 3 位。 如您所见,单体的结果不是很高。
注意: 每次运行训练和测试都会产生不同的结果,因为样本和神经网络的起始初始化将是不同的!
因此,融合当中已经确定了最好的单体分类器。 我们使用以下合并方法在样本 X$test 和 X$test1 上测试它们: 平均和简单多数表决。
b) 平均
#---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.75 0.723 0.739 0.731 1 0.75 0.774 0.760 0.767
关于在脚本中计算的几句话。 利用主要集合 X$test,确定融合的大小 n, 输入 Xtest 和目标 Ytest。 然后,在 foreach 循环中 (仅当索引等于 'bestNN' 索引时),计算这些最佳神经网络的预测,将它们累加,除以最佳神经网络的数量。 将连续变量的输出转换为数字变量 (0,1) 并计算度量衡。 如您所见,分类品质得分远高于那些单体分类器。
与 X$test 之后在 X$test1 上执行相同的测试。 估计品质。
#--6.1 ---test averaging(test1)--------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
分类的品质几乎保持不变,并且仍然很高。 该结果表明,神经网络分类器的融合在训练和修剪之后依然保持较高的分类品质,持续时间 (在我们的示例中,750 根柱线) 比在之前一篇文章 中获得的 DNN 更长。
c) 简单多数表决
我们来确定从融合的最佳分类器获得的预测的度量衡,但是通过简单多数表决来合并。 首先,将最佳分类器的连续预测转换为类标签 (-1/+1),然后累加所有预测标签。 如果总和大于 0,则输出类 1,否则输出 — 类 0。 首先,在 X$test 集合上测试项目:
#--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.745 0.716 0.735 0.725 1 0.745 0.770 0.753 0.761
结果与平均结果几乎相同。 在 X$test1 集合上测试:
#--7.1 --test--voting(test1)-------------------- evalq({ n <- len(Ens) Xtest <- X$test1$x[ , bestF] Ytest <- X$test1$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) Accuracy Precision Recall F1 0 0.761 0.787 0.775 0.781 1 0.761 0.730 0.743 0.737
出乎意料的是,结果比以前的更好,尽管事实上 X$test1 集合位于 X$test 之后。
这意味着依据相同数据上,同一融合的分类品质使用不同合并方法可以有很大变化。
尽管事实上,在融合当中的单体分类器的超参数是凭直觉选择的,且显然不是最优的,但是利用平均和简单多数表决获得了较高且稳定的分类品质。
总结以上所有内容。 示意性地,创建和测试神经网络融合的整个过程可以分为 4 个阶段:
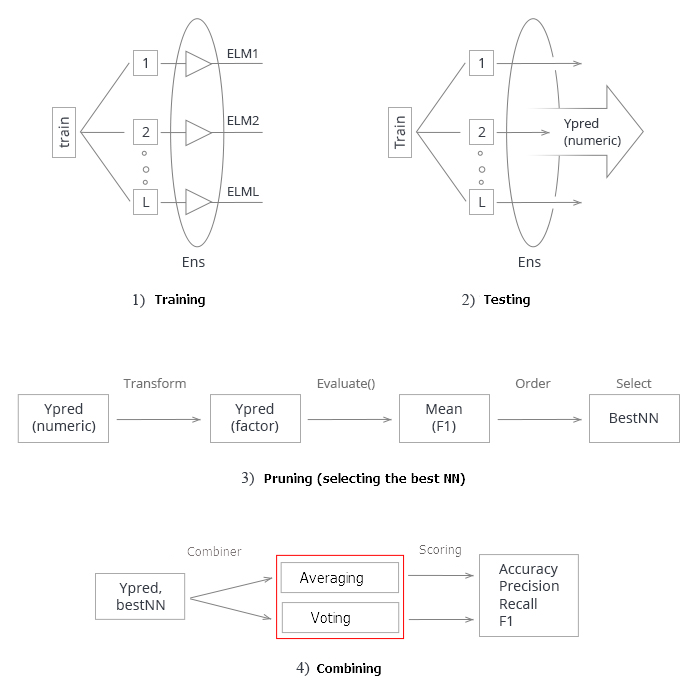
图例3. 利用平均/表决合并器训练和测试神经网络融合的结构
1. 训练融合。 从训练集合中基于随机样本 (bootstrap) 训练 L 神经网络。 获得经过训练的神经网络融合。
2. 在测试集合上测试神经网络的融合。 获得单体分类器的连续预测。
3. 修剪融合,依据某个分类品质标准选择最佳的 n。 在此例中, 它就是 mean(F1).
4. 使用最佳单体分类器的连续预测,在平均或简单多数表决的帮助下将它们合并起来。 之后,确定度量衡。
最后两个步骤 (修剪和合并) 有多个实现选项。 于此同时,成功修剪融合 (最佳识别正确) 可以显著提高性能。 在此情况下,它会查找连续预测的优化阈值并将之转换为数值。 因此,在这些阶段查找最佳参数是一项艰巨的任务。 这些阶段最好能自动执行并得到最佳结果。 我们是否有能力做到这一点,并提高融合的品质得分? 至少有两种方式可以做到这一点,我们会查验它们。
在我们的融合当中单体分类器是 ELM 神经网络。 ELM 的主要特征是它们的属性和品质主要取决于隐藏层神经元权重的随机初始化。 在其它条件相同的情况下 (神经元和激活函数的数量),每次运行训练都会产生一个新的神经网络。
ELM 的这个特性非常适合创建融合。 在融合中,我们不仅用随机值初始化每个分类器的权重,而且还为每个分类器提供单独的随机生成的训练样本。
但是为了选择神经网络的最佳超参数,其品质必须仅取决于给定超参数的变化而非其它任何东西。 否则,搜索的含义就会失去。
一个矛盾出现了: 一方面,我们需要一个尽可能多元化成员的融合,另一方面,融合需要多元但永久的成员。
需要可重现的经久变化。
这可能吗? 我们用一个训练融合的示例来说明这一点。 将利用 "doRNG" (可重现的随机数生成 - Reproducible random number generation RNG) 软件包。 为了重现结果,最好在一个线程中执行计算。
在干净的全局环境中开始新的实验。 再次加载报价和必要的函数库,再次定义和排序源数据,然后重新选择 numFeature 最佳预测器。 在一个脚本中运行它。
#----准备------------- library(anytime) library(rowr) library(elmNN) library(rBayesianOptimization) library(foreach) library(magrittr) library(clusterSim) library(doRNG) #source(file = "FunPrepareData.R") #source(file = "FUN_Ensemble.R") #---准备---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) #--1-Data X------------- list( pretrain = list( x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) ), train = list( x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) ), test = list( x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) ), test1 = list( x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) ) ) -> X #---2--bestF----------------------------------- #require(clusterSim) numFeature <- 10 HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") %$% stopri[ ,1] -> orderX orderX %>% head(numFeature) -> bestF }, env)
所有必要的初始数据都已准备就绪。 训练神经网络的融合:
#---3-----Train---------------------------- evalq({ Xtrain <- X$pretrain$x[ , bestF] Ytrain <- X$pretrain$y setMKLthreads(1) n <- 500 r <- 7 nh <- 5 k <- 1 rng <- RNGseq(n, 12345) Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) k <- k + 1 idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = "sin") } setMKLthreads(2) }, env)
执行期间会发生什么? 定义训练 (Xtrain, Ytrain) 的输入和输出数据,将 MKL 库设置为单线程模式。 通过创建随机数序列 rng 来初始化某些常量,这将在 foreach() 的每次新迭代中初始化随机数生成器。
迭代完成之后,不要忘记将 MKL 设置回多线程模式。 在单线程模式下,计算结果略差。
因此,我们获得了具有不同单体分类器的融合,但在每次训练返回时,融合的这些分类器将保持不变。 多次重复这 4个阶段 (训练/预测/最佳/测试) 的计算,可以很容易地验证这一点。 计算顺序: train/predict/best/test_averaging/test_voting。
#---4-----predict------------------- evalq({ Xtest <- X$train$x[ , bestF] Ytest <- X$train$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] }, env) #---5-----best---------------------- evalq({ numEns <- 3 foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN Score[bestNN] %>% round(3) }, env) # [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713 #---6----test averaging(test)-------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.75 0.711 0.770 0.739 # 1 0.75 0.790 0.734 0.761 #--7 --test--voting(test)-------------------- evalq({ n <- len(Ens) Xtest <- X$test$x[ , bestF] Ytest <- X$test$y foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest) } %>% apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>% apply(1, function(x) sum(x)) -> vot ifelse(vot > 0, 1, 0) -> ClVot Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>% round(3) }, env) # Accuracy Precision Recall F1 # 0 0.749 0.711 0.761 0.735 # 1 0.749 0.784 0.738 0.760
无论这些计算重复多少次 (当然,使用相同的参数),结果将保持不变。 这正是我们需要优化的构成融合的神经网络的超参数。
首先,定义要优化的超参数列表,查找它们的数值范围,并编写适应度函数以便返回优化 (最大化) 标准和融合的预测。 单体分类器的品质受四个参数的影响:
我们罗列出超参数及其数值范围:
evalq({
#type of activation function.
Fact <- c("sig", #: sigmoid
"sin", #: sine
"radbas", #: radial basis
"hardlim", #: hard-limit
"hardlims", #: symmetric hard-limit
"satlins", #: satlins
"tansig", #: tan-sigmoid
"tribas", #: triangular basis
"poslin", #: positive linear
"purelin") #: linear
bonds <- list(
numFeature = c(3L, 12L),
r = c(1L, 10L),
nh <- c(1L, 50L),
fact = c(1L, 10L)
)
}, env)
我们更详细地研究上面的代码。 在这儿,Fact 是可能的激活函数的向量。 列表 bonds 定义要优化的参数及其数值范围。
确定适应度函数。
#---Fitnes -FUN----------- evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
此处是有关该脚本的一些详细信息。 将目标 (Ytrain, Ytest, Ytest1) 的计算移出适应度函数,因为它们在参数搜索期间不会变更。 初始化常量:
n — 融合中神经网络的数量;
numEns — 最佳单体分类器的数量 (numEns*2 + 1),其预测将被合并。
函数 fitnes() 有 4 个正式参数, 应予以优化。 稍后在函数中,训练融合,计算 predict,并逐步确定最佳的 bestNN。 最后,使用平均值合并这些最佳预测并计算度量衡。 该函数返回一个列表,其中包含优化标准 Score = mean(F1) 和预测。 我们将优化这些利用平均合并的融合。 除最终部分外,用来优化以简单多数表决进行融合的超参数的适应度函数是类似的。 您可以自行优化。
我们查验适应度函数的可操作性及其执行时间:
#---------- evalq( system.time( res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2) ) , env) user system elapsed 8.65 0.19 7.86
所有计算约需 9 秒能得到结果。
> env$res$Score [1] 0.761
现在我们可以用 10 个随机初始点和 20 次迭代开始优化超参数。 我们正在寻找最好的结果。
#------ evalq( OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 10, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 23 numFeature = 8.0000 r = 3.0000 nh = 3.0000 fact = 7.0000 Value = 0.7770
按 Value 排序优化历史,并选择 10 个最佳得分:
evalq({
OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init
best.init
}, env)
numFeature r nh fact Value
1 8 3 3 7 0.777
2 8 1 5 7 0.767
3 8 3 2 7 0.760
4 10 7 9 8 0.759
5 8 5 4 7 0.758
6 8 2 7 8 0.756
7 8 6 9 7 0.755
8 8 3 4 8 0.754
9 9 2 13 9 0.752
10 11 2 24 4 0.751
解释所获最佳结果的超参数。 预测器的数量为 8,样本大小为 0.3,隐藏层中的神经元数量为 3,激活函数为 "radbas"。 这再一次证明贝叶斯优化提供了广泛的各式模型,这些模型不太可能凭直觉推导出来。 有必要多次重复优化并选择最佳结果。
因此,已经找到了最优的训练超参数。 用它们来测试融合。
用上述获取的训练过的最佳参数,在测试集合上测试融合。 确定融合的最佳成员,运用平均合并它们的结果并查看最终度量衡。 该脚本如下所示。
在训练神经网络融合时,在优化期间以相同的方式创建神经网络。
#--1-Train--optEns-predict--best--test-average------------------------ evalq({ Ytrain <- X$pretrain$y Ytest <- X$train$y Ytest1 <- X$test$y n <- 500 numEns <- 3 #--BestParams-------------------------- best.par <- OPT_Res$Best_Par %>% unname numFeature <- best.par[1] # 8L r <- best.par[2] # 3L nh <- best.par[3] # 3L fact <- best.par[4] # 7L bestF <- orderX %>% head(numFeature) Xtrain <- X$pretrain$x[ , bestF] setMKLthreads(1) k <- 1 rng <- RNGseq(n, 12345) #---train--- OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } setMKLthreads(2) #---predict--- Xtest <- X$train$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(OptEns[[i]], newdata = Xtest) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- Xtest1 <- X$test$x[ , bestF] foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(OptEns[[i]], newdata = Xtest1)} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>% round(3) -> OptScore caret::confusionMatrix(Ytest1, ensPred) -> cm }, env)
我们来看看融合的 7 个最佳神经网络的结果:
> env$Score[env$bestNN] [1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981 0.7099502
平均最佳神经网络之后的结果:
> env$OptScore Accuracy Precision Recall F1 0 0.778 0.751 0.774 0.762 1 0.778 0.803 0.782 0.793 > env$cm Confusion Matrix and Statistics Reference Prediction 0 1 0 178 52 1 59 212 Accuracy : 0.7784 95% CI : (0.7395, 0.8141) No Information Rate : 0.5269 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5549 Mcnemar's Test P-Value : 0.569 Sensitivity : 0.7511 Specificity : 0.8030 Pos Pred Value : 0.7739 Neg Pred Value : 0.7823 Prevalence : 0.4731 Detection Rate : 0.3553 Detection Prevalence : 0.4591 Balanced Accuracy : 0.7770 'Positive' Class : 0
该结果明显优于融合中任意单体神经网络的结果,并且可与 该系列前一篇文章 中获得的最优参数 DNN 的结果相比。
GitHub/PartVI 包括:

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
