有一门称作“计量金融”的学科,允许使用理论方法和数学物理学研究金融衍生产品的定价模型。
最近我读到一篇文章,文中描述了一种用于技术分析的新指标,该指标结合了量子物理的理念并将它们应用到了金融学。我对它很感兴趣,并决定教授读者如何基于科学论文在 MQL5 实施该指标。
“移动极小化极大”[2] 原文的作者是 Z.K. Silagadze,一位来自 Budker 核物理研究所和新西伯利亚国立大学的量子物理学家。论文和 MQL5 源代码的链接附在本文的末尾。
我从没想过有一天我会和读者讨论这么高深的知识,但在此我不得不解释一下什么是量子隧穿。无意冒犯,但我认为大多数读者对这个领域都相当陌生,所以我将用简单的术语进行描述。首先,让我们用一句话来定义金融时间序列的技术分析的理念基础。我们主要是寻找:
移动极小化极大指标的本意是模仿试图摆脱原子核的量子阿尔法粒子在图表上找出顶部和底部。该问题来自 George Gamov 提出的阿尔法衰变理论 [1]。
一张图片比千言万语还要来的直观,所以我在下面附上一张图表。
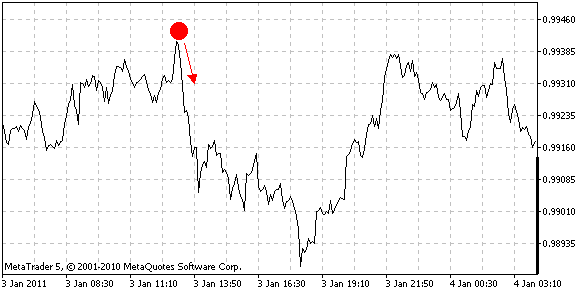
图 1. Forex 价格图表上的假想量子球
想象一下,一个球从山顶抛下,或在我们的示例中从时间序列图表上最近的一个顶部抛下。在经典力学中,它将从障碍物上弹起,并且不可能在最初的障碍物前停下,因为它可能会堵在途中某处。
但根据量子力学和阿尔法衰变理论,这样一个球可以有一个极小但不为零的概率隧穿障碍,到达势阱底部并在那里振荡。
这是在价格图表上寻找局部最小值的一种模拟。Z.K. Silagadze [2] 的论文提出,为降低计算的复杂性而不是解决实际的量子力学问题,模拟量子行为即已足够。我将给出在原文中提出的数学背景,并在稍后以 MQL5 完成实施。
令 ![]() 成为某些时间窗口的价格序列。移动极小化极大是价格序列的非线性变换:
成为某些时间窗口的价格序列。移动极小化极大是价格序列的非线性变换:
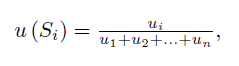
其中 ![]() ,且对于
,且对于 ![]() 定义如下:
定义如下:
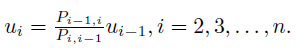
如您所见,这是一个循环关系,第 i 个元素取决于第 i-1 个元素。移动极小化极大序列满足正态化条件,即所有元素的和等于 1。
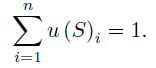
我们将量子球的隧穿概率称为转移概率,因为它们模仿了穿过价格序列的窄障碍的概率,把它们想象成下坡路上的小障碍物:
![]()
其中
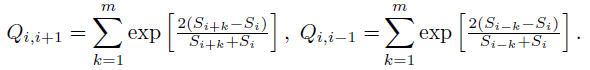
参数 m 是模拟(相反)大多数量子球及其通过小障碍物的能力的平滑窗口的宽度。注重局部最大值的移动极小化极大 d(si) 也可以通过在传递至 exp() 函数的参数前添加负号来构建。
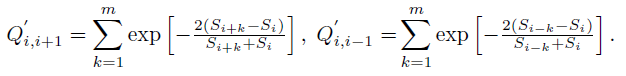
在了解指标的数学基础后,我们以 MQL5 来实施它。我们最好从最后一个等式向上查看。如果您注意到 m 和 n 变量,您会发现,对于一个极小化极大窗口,该指标需要 n+2m 个元素的价格序列数组,并将有大小为 m 个柱的滞后。
这是 Q 变量计算中的 S i+k 和 S i-k 索引造成的。变量 i 从 1 递增至 n 且 k 从 1 递增至 m,因此我们在开始时需要 n+2m 个缓冲区。这可以通过调用以下代码获得:
double S[]; ArrayResize(S,n+2*m); CopyClose(Symbol(),0,0,n+2*m,S);
这将声明双精度型数组,将其大小调整为 n+2m,并从当前交易品种图表最近的柱开始复制最后 n+2m 个柱的收盘值。
接下来我们计算 Q 值。如果您仔细阅读了定义,您将发现,对于分析价格序列的第 i 个元素,我们需要使用价格值变量对 exp() 函数的 m 个结果进行求和。因此,我们需要编写一个从 1 到 n 的循环以计算所有 Q 值:
void calcQii() { int i,k; for(i=0; i<n; i++) { double sqiip1=0; double sqiim1=0; double dqiip1=0; double dqiim1=0; for(k=0; k<m; k++) { sqiip1 += MathExp(2*(S[m-1+i+k]-S[i])/(S[m-1+i+k]+S[i])); sqiim1 += MathExp(2*(S[m-1+i-k]-S[i])/(S[m-1+i-k]+S[i])); dqiip1 += MathExp(-2*(S[m-1+i+k]-S[i])/(S[m-1+i+k]+S[i])); dqiim1 += MathExp(-2*(S[m-1+i-k]-S[i])/(S[m-1+i-k]+S[i])); } sQiip1[i] = sqiip1; sQiim1[i] = sqiim1; dQiip1[i] = dqiip1; dQiim1[i] = dqiim1; } }
如您所见,calcQii 函数为观察到的大小为 n 的价格窗口计算第 i 个 Q 和 Q` 值。S 数组保存价格值,而 sQiip1、sQiim1、dQiip1、dQiim1 用作 Q 和 Q' 的中间计算变量。
概率基于 Q 和 Q` 变量计算,因此我们可以编写从 1 到 n 循环遍历 sQii 和 dQii 数组的另一个函数:
void calcPii() { int i; for(i=0; i<n; i++) { sPiip1[i] = sQiip1[i] / (sQiip1[i] + sQiim1[i]); sPiim1[i] = sQiim1[i] / (sQiip1[i] + sQiim1[i]); dPiip1[i] = dQiip1[i] / (dQiip1[i] + dQiim1[i]); dPiim1[i] = dQiim1[i] / (dQiip1[i] + dQiim1[i]); } }
剩下的就是计算 uSi 和 dSi 元素并将结果放入 uSi 和 dSi 数组:
void calcui() { int i; sui[0] = 1; dui[0] = 1; for(i=1; i<n; i++) { sui[i] = (sPiim1[i]/sPiip1[i])*sui[i-1]; dui[i] = (dPiim1[i]/dPiip1[i])*dui[i-1]; } double uSum = 0; double dSum = 0; ArrayInitialize(uSi, 0.0); ArrayInitialize(dSi, 0.0); for(i=0; i<n; i++) { uSum+=sui[i]; dSum+=dui[i]; } for(i=0; i<n; i++) { uSi[n-1-i] = sui[i] / uSum; dSi[n-1-i] = dui[i] / dSum; } }
为检查正态化条件是否有效,我们可以添加如下代码:
double result=0; for(i=0; i<n; i++) { /* Print("i = "+i+" uSi = "+uSi[i]); */ result+=uSi[i]; } Print("Result = "+ DoubleToString(result));
完成所有计算后,我们需要在指标窗口内进行显示。为此,我们必须声明至少两个指标缓冲区,分别用于 uSi 和 dSi 数组,并将指标类型定义为 DRAW_LINE。
#property indicator_separate_window #property indicator_buffers 2 #property indicator_plots 2 #property indicator_type1 DRAW_LINE #property indicator_type2 DRAW_LINE #property indicator_color1 SeaGreen #property indicator_color2 BlueViolet
然后通过调用 SetIndexBuffer() 函数,我们指定 uSi 和 dSi 数组作为 INDICATOR_DATA 显示:
SetIndexBuffer(0,uSi,INDICATOR_DATA); SetIndexBuffer(1,dSi,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); PlotIndexSetInteger(0,PLOT_SHIFT,-(m-1)); PlotIndexSetInteger(1,PLOT_SHIFT,-(m-1));
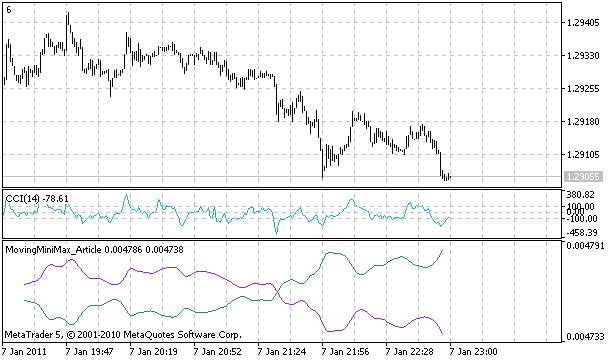
图 2. 实施的移动极小化极大指标
本文介绍的指标可能的应用包括识别支撑线和阻力线以及通过指标的内在平滑识别图标模式。对于支撑线和阻力线而言,它们通过穿越价格序列的移动极小化极大和其移动平均线的移动极小化极大形成。
如果价格通过局部最大值并穿越一条移动平均线,我们获得阻力线。在实施后,我发现该方法受到一些假信号的干扰,所以我附上源代码以供参考,它与如何使用 ChartObjectsLines.mqh 库以通过 MQL5 放入线条有关:
void SR() { // if price goes through local maximum and crosses a moving average draw resistance int i, cnt=0; int rCnt=CopyClose(Symbol(),0,0,n+2*m,S); for (i=n-2; i>=0; i--) if (uSi[i]<uSi_MA[i] && uSi[i+1]>=uSi_MA[i+1]) { Print("Resistance at " + i); CChartObjectHLine *line=new CChartObjectHLine(); line.Create(0, "MiniMaxResistanceLine:"+IntegerToString(cnt), 0, S[i]); line.Color(LightSkyBlue); line.Width(1); line.Background(true); line.Selectable(false); cnt++; } // if price goes through local minimum and crosses a moving average draw support for (i=n-2; i>=0; i--) if (dSi[i]<dSi_MA[i] && dSi[i+1]>=dSi_MA[i+1]) { Print("Support at " + i); CChartObjectHLine *line=new CChartObjectHLine(); line.Create(0, "MiniMaxSupportLine:"+IntegerToString(cnt), 0, S[i]); line.Color(Tomato); line.Width(1); line.Background(true); line.Selectable(false); cnt++; } }
有趣的是,我发现指标在识别指定时间窗口的局部短期最小值和最大值方面运行良好。过滤移动极小化极大的最高和最低读数之间的点差,并将它们标示为短期涨势或跌势的前兆即已足够。
我们可以根据其他指标和资金管理利用这一行为,构建盈利的“EA 交易”。
为了在当前时间窗口中标示最高读数,我们可以使用额外的指标缓冲区,以在每次点差最大时显示向上和向下的箭头。此外,为使指标更加美观,我决定使用 MQL5 的新功能:彩色直方图。下降趋势和上升趋势采用不同的颜色着色,而趋势变化通过黄色的柱标示。
为了在两个缓冲区之间使用彩色直方图,我们必须使用 2 个数据缓冲区和 1 个用于颜色索引的缓冲区。请注意如何定义绘图。总共有 5 个指标缓冲区,并为彩色直方图定义了 3 种颜色。
//+------------------------------------------------------------------+ //| MovingMiniMax.mq5 | //| Copyright 2011, Investeo.pl | //| http://Investeo.pl | //+------------------------------------------------------------------+ #property copyright "Copyright 2011, Investeo.pl" #property link "http://Investeo.pl" #property description "Moving Mini-Max indicator" #property description "proposed by Z.K. Silagadze" #property description "from Budker Institute of Nuclear Physics" #property description "and Novosibirsk State University" #property description "Original paper can be downloaded from:" #property description "http://arxiv.org/abs/0802.0984" #property version "0.6" #property indicator_separate_window #property indicator_buffers 5 #property indicator_plots 3 #property indicator_type1 DRAW_COLOR_HISTOGRAM2 #property indicator_type2 DRAW_ARROW #property indicator_type3 DRAW_ARROW #property indicator_color1 Chartreuse, OrangeRed, Yellow #property indicator_color2 RoyalBlue #property indicator_color3 RoyalBlue #property indicator_width1 5 #property indicator_width2 4 #property indicator_width3 4
请注意,直方图有两个 INDICATOR_DATA 类和一个INDICATOR_COLOR_INDEX 类的缓冲区。缓冲区必须严格按照下述顺序设置:首先设置数据缓冲区,之后定义颜色索引缓冲区。
SetIndexBuffer(0,uSi,INDICATOR_DATA); SetIndexBuffer(1,dSi,INDICATOR_DATA); SetIndexBuffer(2,trend,INDICATOR_COLOR_INDEX); SetIndexBuffer(3,upArrows,INDICATOR_DATA); SetIndexBuffer(4,dnArrows,INDICATOR_DATA); PlotIndexSetDouble(0,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(1,PLOT_EMPTY_VALUE,0.0); PlotIndexSetDouble(2,PLOT_EMPTY_VALUE,0.0); PlotIndexSetInteger(1,PLOT_ARROW,234); PlotIndexSetInteger(2,PLOT_ARROW,233);
缓冲区 0、1、2 用于彩色直方图,缓冲区 3 和 4 用于箭头显示。
着色算法实施如下:
if (upind<dnind) { for (i=0; i<upind; i++) trend[i]=0; for (i=upind; i<dnind; i++) trend[i]=1; for (i=dnind; i<n; i++) trend[i]=0 ; } else { for (i=0; i<dnind; i++) trend[i]=1; for (i=dnind; i<upind; i++) trend[i]=0; for (i=upind; i<n; i++) trend[i]=1; } trend[upind] = 2; trend[dnind] = 2;
我将最终结果的屏幕截图附在下面:
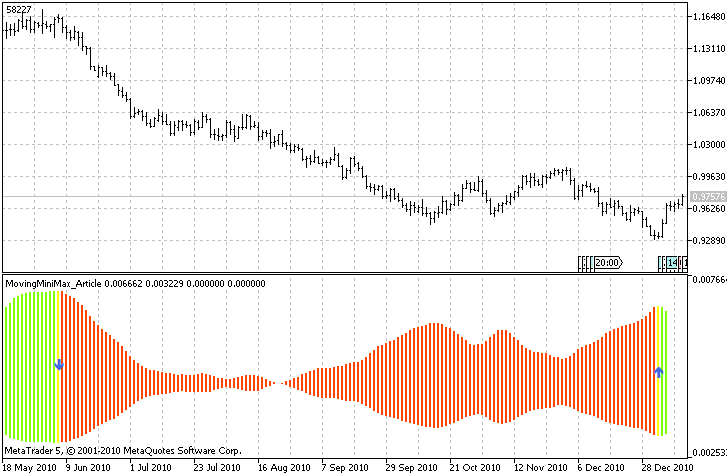
图 3. 移动极小化极大指标的最终版本
切记,每次有新柱出现时便为指定时间窗口计算下降趋势和上升趋势的值,这就是调用移动极小化极大指标的原因。
虽然该指标滞后 m 个柱,但它在当前时间窗口中提供了极佳的趋势概况,以及如何把握市场的“脉搏”的诠释。
我确信该指标可为您带来盈利。
我介绍了一个用于技术分析的新指标的数学基础及其通过 MQL5 的实施。
Z.K. Silagadze 所著的原作请参见 http://arxiv.org/abs/0802.0984。随附源代码可供读者下载。
我希望,在未来能够有机会为读者介绍更多感兴趣的技术指标以及它们的 MQL5 实施。
1. G.Gamov,《阿尔法衰变理论》。
2. Z.K. Silagadze,《移动极小化极大 - 技术分析的新指标》。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
