指标的快速计算是一项至关重要的任务。可通过不同的方法加快计算。有很多文章讨论这一问题。
现在,我们检验用于加快计算,甚至有时能简化代码本身的 3 种方法。介绍的所有方法都是算法方面的,即我们不会减少历史深度或启用处理器单元的额外内核。我们将直接优化算法。
基本指标
用于显示所有 3 种方法的指标是一个线性回归指标。它在每一根柱创建回归函数(依据定义的最后柱的数量)并显示在该柱的函数值。如此一来,我们得到一条实线:
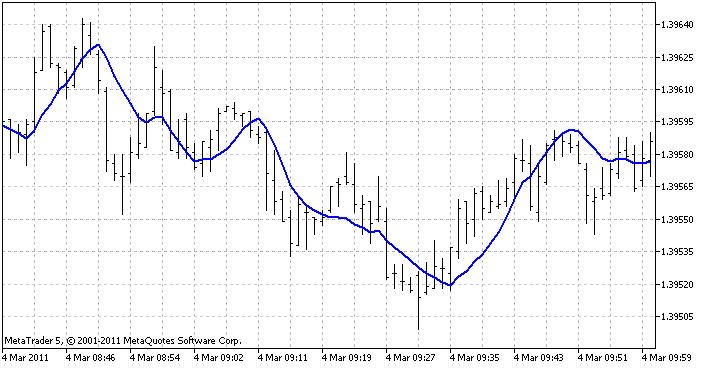
这是指标在客户端中的样子
线性回归等式如下所示:
![]()
在我们的例子中,x 是柱的数量,y 是价格。
所提等式的变换系数按以下方式计算:
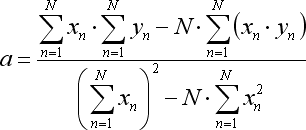
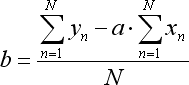
其中 N 是用于形成回归线条的柱的数量。
以下是这些等式在 MQL5 中的样子(在所有历史柱循环内):
// Finding intermediate values-sums Sx = 0; Sy = 0; Sxx = 0; Sxy = 0; for (int x = 1; x <= LRPeriod; x++) { double y = price[bar-LRPeriod+x]; Sx += x; Sy += y; Sxx += x*x; Sxy += x*y; } // Regression ratios double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx); double b = (Sy - a * Sx) / LRPeriod; lrvalue = a*LRPeriod + b;
本文附带了指标的完整代码。它还包含了本文介绍的所有方法。因此,必须在指标设置中选择 "Standard"(标准)计算方法:
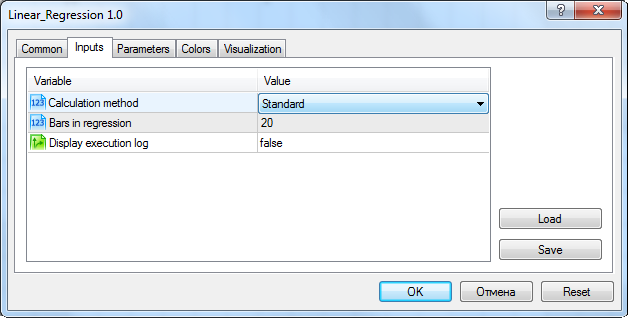
在图表中设置时的指标输入参数设置窗口
有很多指标在每一根柱计算某些柱序列的值的总和。并且这个序列在每一根柱都会偏移。最著名的例子是移动平均线 (MA)。它计算最后 N 根柱的总和,然后将得到的值除以柱的数量。
我认为,只有很少的人知道有一种极好的方式来显著加速此类移动总和的计算。当我发现这种方法已经在 MetaTrader 4 和 5 常规 MA 指标中使用后,在相当长的时间里,我已经在我的指标里使用这种方法。(它不是我发现开发人员正确优化 MetaTrader 指标的第一个例子。很久以前,我正在寻找快速峰谷指标,有一个常规指标经证明比大多数外部指标更有效。顺便说一句,所提的论坛主题也包含峰谷指标优化方法,以备不时之需。)
现在,我们将返回到移动总和。让我们为相邻的两根柱比较计算出来的总和。下图说明这些总和具有相当可观的共同部分(以绿色显示)。为第 0 根柱计算出来的总和与第 1 根柱的总和的唯一差别在于总和不包括一根过期的柱(左边红色的一根),但是包含一根新柱(右边蓝色的一根):
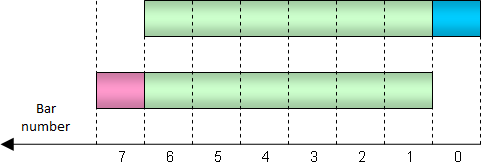
偏移一根柱期间总和不包括的值和包括的值
因此,在为第 0 根柱计算总和时不需要再次为所有必需的柱计算总和。我们可以只采用第 1 根柱的总和,然后减去一个值,再添加一个新的值。只需要两次算术运算。使用此类方法,我们可以相当显著地加快指标计算。
在移动平均线中通常均采用此类方法,因为指标仅在其缓存中保持所有平均值。不过是将总和除以包含在总和中的柱数 N 得到的值。通过将缓存中的一个值乘以 N,我们可以轻松地得到任意柱的总和,然后再应用上述方法。
现在,我将向您展示如何在更加复杂的指标 – 线性回归中应用此方法。您已经看到用于计算回归函数变换系数的等式包含四个总和:x、y、x*x、x*y。这些总和的计算必须保存在缓存中。为此,必须为指标中的每个总和分配缓存:
double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];
缓存不必出现在图表中。MetaTrader 5 有一个特殊的缓存类型 – 用于中间计算。我们将在 OnInit 中用它来分配缓存数量:
SetIndexBuffer(1, ExtBufSx, INDICATOR_CALCULATIONS); SetIndexBuffer(2, ExtBufSy, INDICATOR_CALCULATIONS); SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS); SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);
现在,标准线性回归计算代码将变为:
// (The very first bar was calculated using the standard method) // Previous bar int prevbar = bar-1; //--- Calculating new values of intermediate totals // from the previous bar values Sx = ExtBufSx [prevbar]; // An old price comes out, a new one comes in Sy = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; Sxx = ExtBufSxx[prevbar]; // All the old prices come out once, a new one comes in with an appropriate weight Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod; //--- // Regression ratios (calculated the same way as in the standard method) double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx); double b = (Sy - a * Sx) / LRPeriod; lrvalue = a*LRPeriod + b;
本文附带了指标的完整代码。必须在指标设置中设置 "Moving Totals"(移动总和)计算方法。
数学发烧友将感激此方法。在复杂的等式中,经常可以发现某些部分是某些其他已知等式的右边部分。这样提供了用它们的左边部分代替这些部分的可能(通常仅包含一个变量)。换言之,我们可以简化复杂的等式。有这样的可能,此简化等式的某些元素已经作为指标实现了。在这种情况下,包含该等式的指标代码可以得到相当程度的简化。
这样一来,我们至少获得了更加节省空间的简单代码。在某些情况下它也更快,如果在代码中实施的指标得到良好的速度优化的话。
似乎线性回归等式也可以简化,并且可用几个 MetaTrader 5 标准指标的初始化来代替其计算。在其不同的计算模式中,很多元素在移动平均指标中计算:
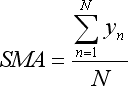
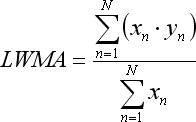
注意,LWMA 的等式仅在我们从 1 到 N 以过去到将来的升序枚举参与回归的柱时才成立:
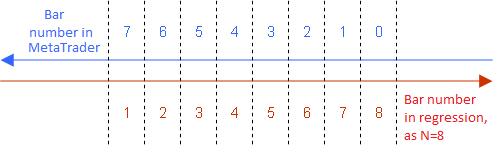
为使用 LWMA 指标而枚举回归所用的柱的传统方式
因此,必须在所有其他等式中使用相同的枚举。
让我们继续该方法:
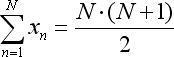
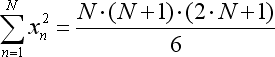
![]()
因此,最后五个等式允许我们替换变换系数计算等式 a 和 b 中以及回归等式本身中的所有变量。在完成所有替换之后,我们将得到一个用于计算回归值的全新等式。它将仅包括移动平均指标值和数字 N。在对其元素的所有约减完成之后,我们将得到一个极好的等式:
![]()
此等式替换了在线性回归基本指标中执行的所有计算。显然,采用该等式的指标代码将节省很多空间。在“速度比较”一章中,我们也将发现代码是否运行得更快。
指标的指定部分:
double SMA [1]; double LWMA[1]; CopyBuffer(h_SMA, 0, rates_total-bar, 1, SMA); CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA); lrvalue = 3*LWMA[0] - 2*SMA[0];
LWMA 和 SMA 指标是在 OnInit 中初始创建的:
h_SMA = iMA(NULL, 0, LRPeriod, 0, MODE_SMA, PRICE_CLOSE); h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);
本文附带了完整代码。必须在指标设置中设置 "Simplification"(简化)计算方法。
注意:在这个方法中,我们使用客户端内置的指标,即使用函数 iMA 并选择适当的平滑方法代替 iCustom。这很重要,因为在理论上,内置指标应非常快速地运行。客户端还内置了某些其他标准指标(它们是通过诸如 iMA 的具有 "i" 前缀的函数创建的)。在使用简化方法时,最好将等式简化到这些指标。
这个方法的理念是可以用近似计算所需值的更快的指标代替在 EA 交易中使用的“重”指标。使用这个方法,您能够更快地测试您的策略。毕竟在调试阶段预测精度并不是如此重要。
此方法也可用与一个有效的策略配合使用,对参数进行大体优化。这样能够迅速找出参数的有效值区域。然后可以继续通过“重”指标进行精细调整。
此外,近似计算似乎足以让一个策略正常地工作。在这种情况下,“变轻”的指标也可在实际交易中使用。
可以为线性回归开发一个快速等式,该等式具有与回归类似的效果。例如,我们可以将回归柱分为两个组,为每个组计算平均值,通过这两个平均点绘制一条线,然后在最后一根柱上定义直线的值:
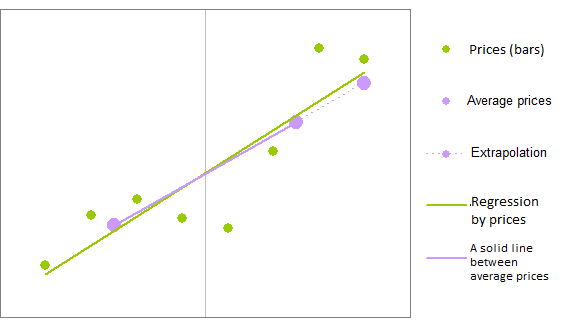
点被分为两个组 - 左边的一组和右边的一组 - 并执行计算
此计算包含的算术运算比回归等式要少。这是加快计算的方式。
// The interval midpoint int HalfPeriod = (int) MathRound(LRPeriod/2); // Average price of the first half double s1 = 0; for (int i = 0; i < HalfPeriod; i++) s1 += price[bar-i]; s1 /= HalfPeriod; // Average price of the second half double s2 = 0; for (int i = HalfPeriod; i < LRPeriod; i++) s2 += price[bar-i]; s2 /= (LRPeriod-HalfPeriod); // Price excess by one bar double k = (s1-s2)/(LRPeriod/2); // Extrapolated price at the last bar lrvalue = s1 + k * (HalfPeriod-1)/2;
本文附带了指标的完整代码。必须在指标设置中设置 "Approximating"(近似)计算方法。
现在,让我们分析这种近似与原来的计算有多接近。为此,我们必须在一张图表上设置分别采用标准计算方法和近似计算方法的指标。我们还必须添加任何已知的与回归有一点相似关系的其他指标。然而,仍然应使用过去的柱计算某些趋势。移动平均正好符合这些要求(我使用 LWMA 而不是 SMA - 它更类似回归图表)。此外,我们能够评估我们是否有良好的近似。我认为它还不错:
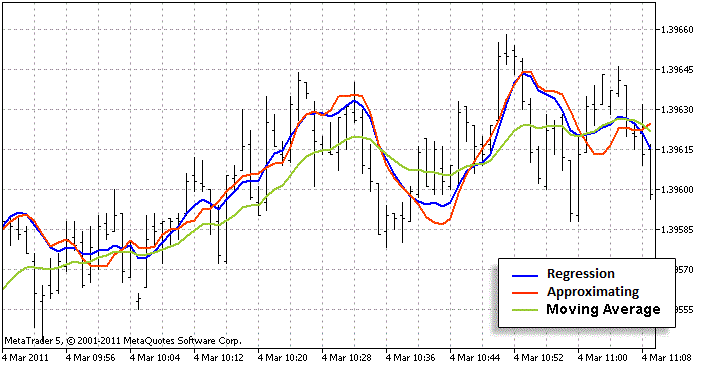
红线比绿线更接近蓝线。这意味着近似算法很好
可以在指标参数启用日志显示:
设置指标以评估执行速度
在这个例子中,指标将在 EA 交易消息日志中显示用于速度评估的所有必要数据:开始处理 OnInit() 事件的时间以及 OnCalculate() 的结束时间。我将解释为什么必须用这两个值评估速度。在任何方法中,OnInit() 代理几乎立即执行;并且几乎在任何方法中,OnCalculate() 在 OnInit() 之后立即开始。唯一例外是一种在 OnInit() 中创建 SMA 和 LWMA 指标的简化方法。在使用所提及的方法时(并且仅限于该情形),在 OnInit() 结束和 OnCalculate() 开始之间存在延迟:

在客户端的 EA 交易日志中按指标显示的执行日志
这意味着这个延迟是新创建的在那个时候执行相同计算的 SMA 和 LWMA 造成的。也必须考虑此计算的持续时间,因此,我们将“不间断地”评估所有时间 - 从回归指标初始化直到其计算的结束。
为了更加精确地指出不同方法之间的速度差异,所有评估都是采用数据量巨大的数组进行的 – M1 时间框架和最大的可访问历史深度。这超过 400 万根柱。每种方法将被评估两次:在回归中分别使用 20 根柱和 2000 根柱。
结果如下所示:
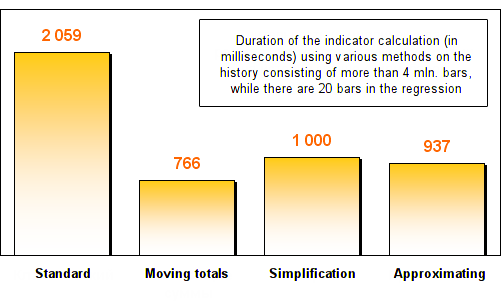
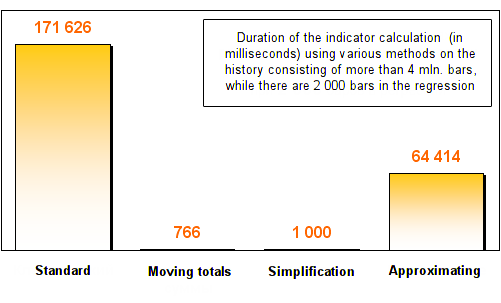
如您所见,与标准回归计算方法相比,所有三种优化方法都展示出至少两倍的速度增加。在回归中增加柱数之后,移动总和及简化方法展示出令人难以置信的速度。它们比标准方法快了几百倍!
我应该指出,这两种方法需要的计算时间几乎保持不变。可以很容易地解释这个事实:无论我们用于创建回归的柱有多少,在移动总和方法中只执行两个操作 - 删除旧的柱,添加新的柱。没有任何取决于回归长度的循环。因此,即使回归包含 20000 根柱或 200000 根柱,与 20 根柱相比,方法执行时间将不会增加多少。
简化方法在其等式中使用不同模式的移动平均。如我已经指出的,此指标可以轻松地通过移动总和方法得到优化,并且已经被客户端开发人员所采用。毫无疑问,简化方法的执行时间在回归长度增大时也不会改变。
在我们的实验中,移动总和方法经证明是最快的计算方法。
某些交易者只是干坐着,等待他们的交易系统的另一个参数优化过程在他们的测试程序中结束。但是还有一些交易者,他们在那个时间进行交易并赚钱。通过所述方法获得的计算速度清楚地解释了为什么这两类交易者之间会有如此之大的差异。这也解释了为什么注意交易算法的质量是如此重要。
它与您是为客户端或自己编写程序还是向第三方程序员订购程序(例如在 "Jobs"(工作机会)部分的帮助下)无关。在任何情形下,您都不仅可以获得有效的指标和策略,并且还能获得快速运行的指标和策略,如果您准备好付出一些努力或支付部分金钱的话。
如果您使用任何算法加速方法,则与标准算法相比较,您将获得十倍甚至百倍的速度优势。举例而言,这意味着您能够快一百倍地在测试程序中优化您的交易策略参数。使其更仔细、更频繁地交易。无需赘言,这将使您的交易收入增加。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...